Предмет: Алгебра,
автор: Аноним
помогите решить пожалуйста,очень срочно
Приложения:

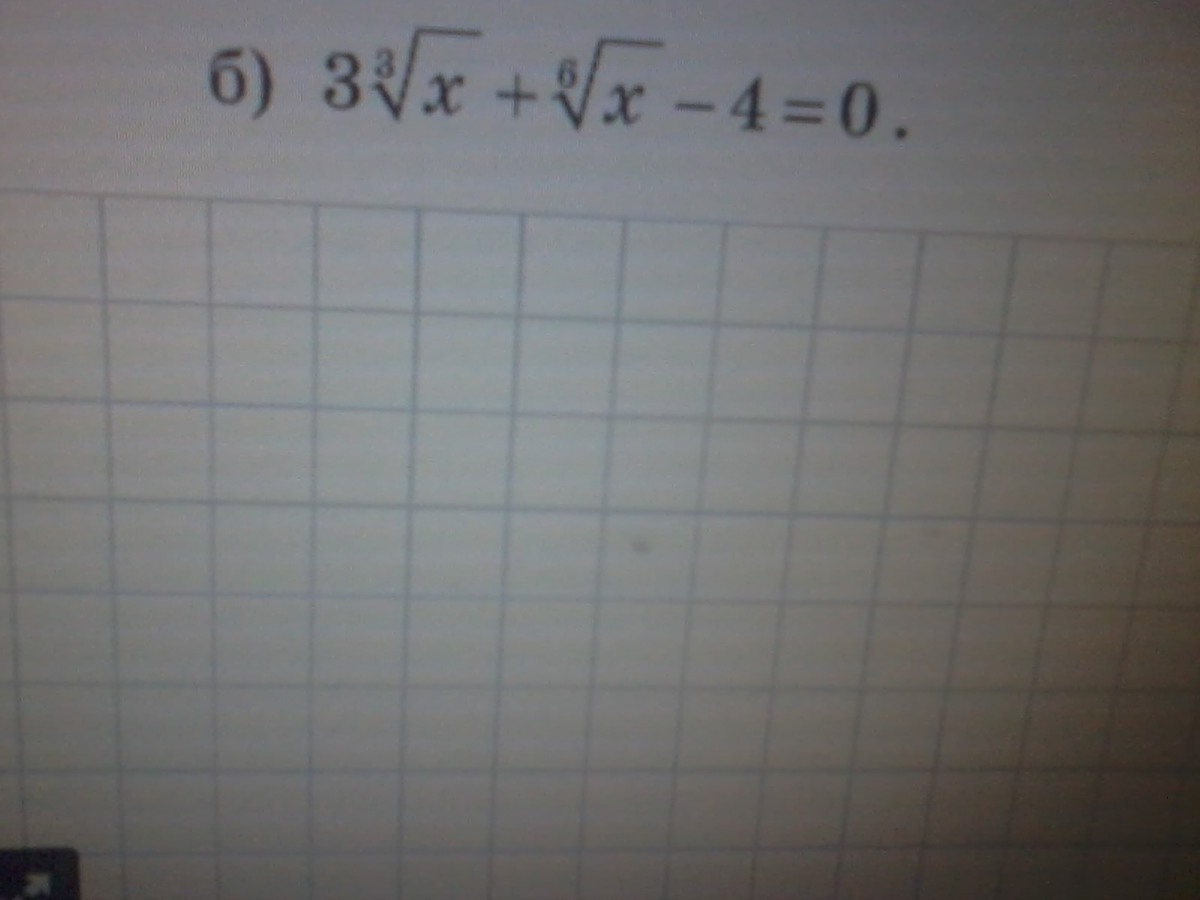
Ответы
Автор ответа:
0
б) Сделаем замену: ![sqrt[6]{x}=t>0 sqrt[6]{x}=t>0](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7Bx%7D%3Dt%26gt%3B0)
Тогда:![sqrt[3]{x}=t^{2} sqrt[3]{x}=t^{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7Bx%7D%3Dt%5E%7B2%7D)


 - посторонний корень
- посторонний корень
Вернемся обратно к замене:
![sqrt[6]{x}=1 sqrt[6]{x}=1](https://tex.z-dn.net/?f=sqrt%5B6%5D%7Bx%7D%3D1)
 - ответ
- ответ
а) ОДЗ:
 ,
, 
 ,
, 
 ,
, 
Общее решение ОДЗ:
Возведем обе части уравнения в квадрат:




 - посторонний корень
- посторонний корень
 - ответ
- ответ
Тогда:
Вернемся обратно к замене:
а) ОДЗ:
Общее решение ОДЗ:
Возведем обе части уравнения в квадрат:
Похожие вопросы
Предмет: Литература,
автор: tsarevsvyat2
Предмет: Математика,
автор: Askdkffkfkmmx193944
Предмет: История,
автор: kseniiagib
Предмет: История,
автор: Katyhadley