Предмет: Алгебра,
автор: nastya1997d
решить уравнение.
помогите пожалуйста, может кто понимает
x^4-3x^3+2x^2-3x+1=0
Ответы
Автор ответа:
0
Приложения:
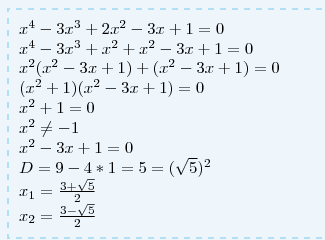
Автор ответа:
0
огромнейшее спасибо, настя)
Автор ответа:
0
не за что)
Автор ответа:
0
Выражение x^4-3x^3+2x^2-3x+1=0 раскладываем на множители:
(х²+1)(х²-3х+1) = 0.
Нулю может быть только второй множитель:
Решаем уравнение x^2-3*x+1=0:
Ищем дискриминант:D=(-3)^2-4*1*1=9-4=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-3))/(2*1)=(√5+3)/2=√5/2+3/2=√5/2+1.5~~2.6180339887499;
x_2=(-√5-(-3))/(2*1)=(-√5+3)/2=-√5/2+3/2=-√5/2+1.5~~0.3819660112501.
(х²+1)(х²-3х+1) = 0.
Нулю может быть только второй множитель:
Решаем уравнение x^2-3*x+1=0:
Ищем дискриминант:D=(-3)^2-4*1*1=9-4=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-3))/(2*1)=(√5+3)/2=√5/2+3/2=√5/2+1.5~~2.6180339887499;
x_2=(-√5-(-3))/(2*1)=(-√5+3)/2=-√5/2+3/2=-√5/2+1.5~~0.3819660112501.
Приложения:
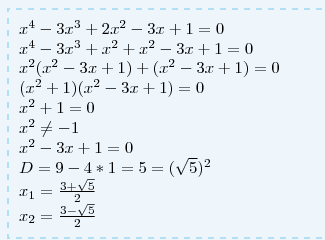
Похожие вопросы
Предмет: Математика,
автор: stasikep
Предмет: История,
автор: Baibekova
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: СалаховаМарина