Question

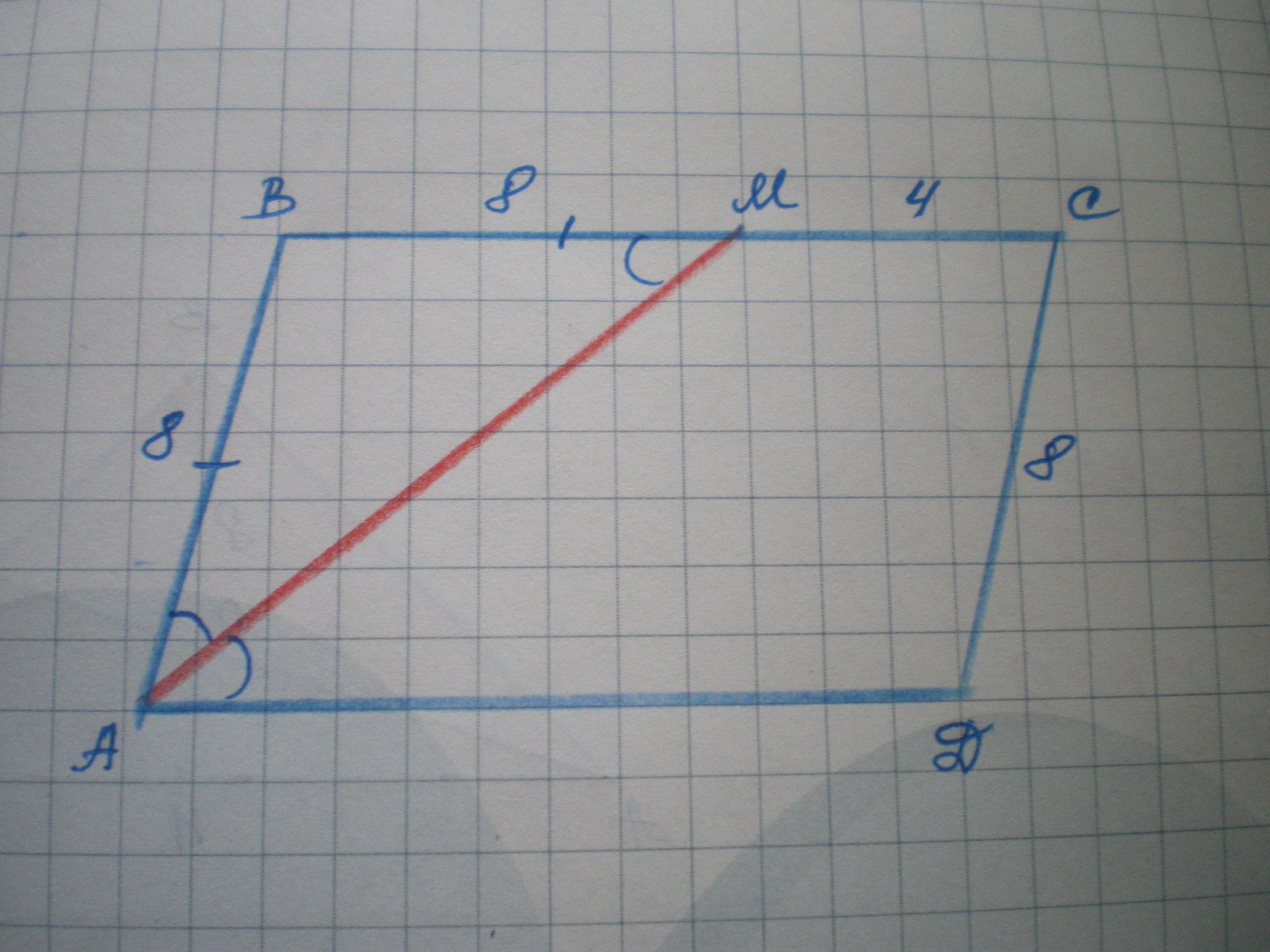
НИКТО НЕ МОЖЕТ РЕШИТЬ!!!! на стороне bc параллелограмма abcd выбрана точка M так,что AB=BM докажите a)что AM-биссектриса угла BAD b) найдите периметр параллелограмма,если CD=8см,CM=4см

Answer 1

а) Так как AB = BM, то треугольник ABM - равнобедренный и ∠BAM = ∠BMA.
Так как BC || AD, то ∠BMA = ∠MAD, как скрещивающиеся углы при параллельных прямых.
Из этих двух утверждений следует, что ∠BAM = ∠MAD, то есть AM - биссектриса ∠BAD по определению.

б) Периметр параллелограмма P = 2 * (BC + CD) = 2 * (BM + MC + CD) = 2 * (AB + MC + CD) = 2 * (CD + MC + CD) = 40 см

Answer 2

ABM - равнобед треугольник, след. стороны при основании у него равны.

BC || AD при секущей AM, след.  угл MAD  равен углу ABM 

Т.К.  угл BMA равен углу BAM  и  MAD, то выходит, что MA - бис.

 

BC= 8 + 4 = 12 ( т.к. BM = AB и MC = 4)

P пар = 2(a+b) = 2( 12 + 8) = 40

Answer 3

а) Так как AB = BM, то Δ ABM - равнобедренный и ∠BAM = ∠BMA.

∠BMA = ∠MAD, как внутренние накрест лежащие углы при АD║ВС и секущей АМ.

Из этих двух утверждений следует, что ∠BAM = ∠MAD, то есть AM - биссектриса ∠BAD по определению.

б)  ВС=ВМ+СМ; ВМ=АВ=8 см;  ВС=8+4=12 см.;  АД=ВС=12 см.  

P (АВСD) = 2 * (BC + CD) = 2 * (12+8) = 40 см.