Предмет: Геометрия,
автор: nata3103
SABCD четырехугольная пирамида.точка T лежит на ребре SB, точки P и E середины ребер AD и CDсоответственно.а) постройте сечение пирамиды плоскостьюTPE б)по какой прямой пересекаются плоскости TPE и SAC?
Ответы
Автор ответа:
0
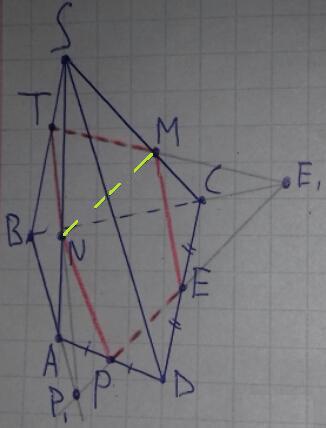
а)
PE ∩ AB = P₁ т.к. PE, AB ⊂ (ABC).
PE ∩ BC = E₁ т.к. PE, BC ⊂ (ABC).
P₁ и E₁ ∈ PE ⊂ (TPE) ⇒ P₁ и E₁ ∈ (TPE).
P₁ ∈ AB ⊂ (ABS) и T ∈ SB ⊂ (ABS) соединяем две точке, которые лежат в одной плоскости (ABS).
P₁T ∩ SA = N ∈ (TPE) т.к. T, P₁ ∈ (TPE).
E₁ ∈ BC ⊂ (BCS) и T ∈ SB ⊂ (BCS) соединяем две точке, которые лежат в одной плоскости (BCS).
E₁T ∩ SC = M ∈ (TPE) т.к. T, E₁ ∈ (TPE).
TMEPN - нужное сечение.
б)
M, N ∈ (TPE);
M ∈ SC ⊂ (SAC) ⇒ M ∈ (SAC);
N ∈ SA ⊂ (SAC) ⇒ N ∈ (SAC).
Получается, что (TPE) ∩ (SAC) = MN
Ответ: MN.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: abdin200223
Предмет: Математика,
автор: ElenaGilbert2005
Предмет: Химия,
автор: zhanberkembaeva
Предмет: Биология,
автор: Arinok19
Предмет: Математика,
автор: makarowtolya197