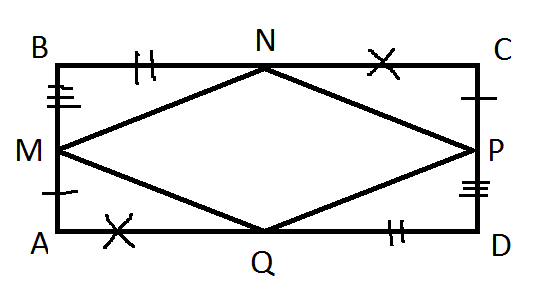
На сторонах АВ ВС СD DA четырёхугольника АВСD отмечены соответственно точки MNPQ так,что АМ=СР BN=DQ BM=DP NC=QA.Доказать, что ABCD и NMPQ-паролеллограммы
Ответы
BC=BN+NC; AD=AQ+QD, т.к. BN=DQ, а NC=QA, то BC=AD.
Аналогично BA=CD.
ABCD- параллелограмм, т.к. AB=CD, BC=AD ( если противоположные стороны в 4-угольнике попарно равны, то этот 4-угольник - параллелограмм).
Рассмотрим ▲MBN и ▲PDQ.
1) BN=DQ - по условию.
2) BM=DP - по условию.
3) ∠B =∠D, т.к. они противоположные углы в параллелограмме равны.
▲MBN =▲PDQ по 2 сторонам и углу между ними.
Значит MN=QP, как соответствующие элементы в равных треугольниках.
Рассмотрим ▲NCP и ▲MAQ.
1) АМ=СР - по условию.
2) NC=QA - по условию.
3) ∠A= ∠C, т.к. они противоположные углы в параллелограмме.
▲NCP =▲MAQ по 2 сторонам и углу между ними.
Значит NP=MQ, как соответствующие элементы в равных треугольниках.
MN=QP,NP=MQ , значит MNPQ - параллелограмм ( если противоположные стороны в 4-угольнике попарно равны, то этот 4-угольник - параллелограмм).
Чертеж получился корявенький, но думаю суть ты уловил. Только рисуй именно параллелограмм, а не прямоугольник, учителя обычно к этому жутко придераются, а у меня в Paint был только прямоугольник.