Предмет: Алгебра,
автор: Alesya83
Очень срочно! Помогите! Найти промежутки возрастания и убывания.
Приложения:
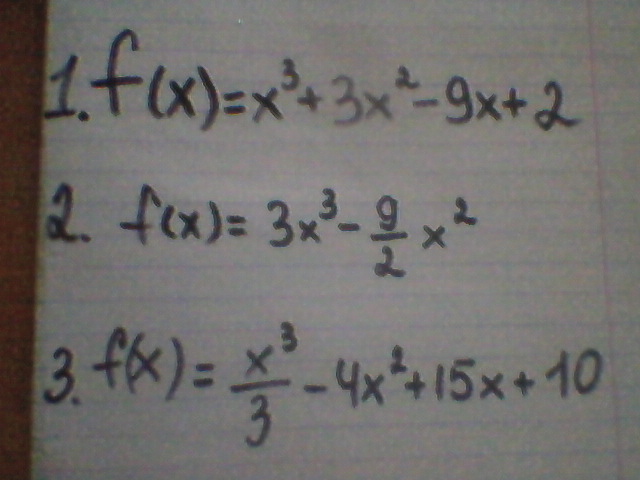
Ответы
Автор ответа:
0
1. f'(x)=(x^3+3x^2-9x+2)'=3x^2+6x-9
3x^2+6x-9=0
x^2+2x-9=0
Д=4-4*(-3)=16=4^2
x1=(-2+4)/2=1
x2=(-2-4)/2=-3
Функция возрастает: x∈(-бесконечность; -3] [1;+бесконечность)
Функция убывает: x∈[-3;1]
2. f'(x)=(3x^3-(9x^2)/2)'=9x^2-9x
9x^2-9x=0
9x(x-1)=0
9x=0
x1=0
x-1=0
x2=1
Функция возрастает: x∈(-бесконечность;0] [1;+бесконечность)
Функция убывает: x∈[0;1]
3. f'(x)=(x^3/3-4x^2+15x+10)'=x^2-8x+15
x^2-8x+15=0
Д=64-4*15=4=2^2
x1=(8+2)/2=5
x2=(8-2)/2=3
Функция возрастает: x∈(-бесконечность;3] [5;+бесконечность)
Функция убывает: x∈[3;5]
3x^2+6x-9=0
x^2+2x-9=0
Д=4-4*(-3)=16=4^2
x1=(-2+4)/2=1
x2=(-2-4)/2=-3
Функция возрастает: x∈(-бесконечность; -3] [1;+бесконечность)
Функция убывает: x∈[-3;1]
2. f'(x)=(3x^3-(9x^2)/2)'=9x^2-9x
9x^2-9x=0
9x(x-1)=0
9x=0
x1=0
x-1=0
x2=1
Функция возрастает: x∈(-бесконечность;0] [1;+бесконечность)
Функция убывает: x∈[0;1]
3. f'(x)=(x^3/3-4x^2+15x+10)'=x^2-8x+15
x^2-8x+15=0
Д=64-4*15=4=2^2
x1=(8+2)/2=5
x2=(8-2)/2=3
Функция возрастает: x∈(-бесконечность;3] [5;+бесконечность)
Функция убывает: x∈[3;5]
Похожие вопросы
Предмет: Информатика,
автор: misharasha05
Предмет: Английский язык,
автор: dinaabiltaj
Предмет: Русский язык,
автор: amirkonysbaj26
Предмет: Математика,
автор: новичок23
Предмет: Алгебра,
автор: glushakovanatas