Предмет: Алгебра,
автор: Oleinikovanyur
Найти y'' и d^2y
Y=lnctg4x
Ответы
Автор ответа:
0
Приложения:
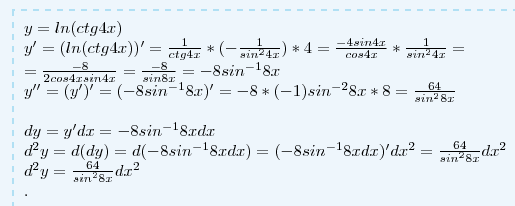
Похожие вопросы
Предмет: Русский язык,
автор: IceStarsYT
Предмет: Биология,
автор: aaulymdauletkalieva
Предмет: Математика,
автор: makskurbanov447
Предмет: Математика,
автор: malinka75
Предмет: Алгебра,
автор: anastsaass