Предмет: Алгебра,
автор: lerasanjura
1) logx(2x+3)<2
2) log4(2x-1)<= log4(x-3)
3) lg^2(10x)-lgx >=3
4) (lg (sqrt(x+1)+1)) / lg^3(sqrt x-40) = 3
как решать?пожалуйста...
Ответы
Автор ответа:
0
Приложения:

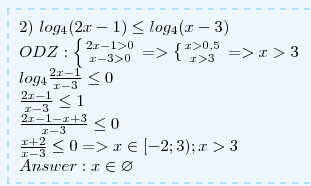


Автор ответа:
0
В 1 не учтено основание логарифма,в 4 степень 3 у самого логарифма,а не у выражения
Автор ответа:
0
В 1 учтено основание логарифма, посмотри внимательно.
Автор ответа:
0
Можешь объяснить откуда 1/3?
Автор ответа:
0
Ага, вижу, 9ка должна быть, тогда будет 1 решение в действительной области, и то, приближенное.
В любом случае в условии п.4 явно что-то намутили)
В любом случае в условии п.4 явно что-то намутили)
Автор ответа:
0
1)2x+3>0⇒2x>-3⇒x>-1,5 U x>0 U x≠1⇒x∈(0;1) U (1;∞)
a)x∈(0;1)
2x+3>x²⇒x²-2x-3<0
x1+x2=2 U x1*x2=-3⇒x1=-1 U x2=3
-1<x<3 U x∈(0;1)⇒x∈(0;1)
b)x∈(1;∞)
2x+3<x²⇒x²-2x-3>0
x1+x2=2 U x1*x2=-3⇒x1=-1 U x2=3
x<-1 U x>3 U x∈(1;∞)⇒x∈(3;∞)ответ x∈(0;1) U (3;∞)
2)2x-1>0⇒2x>1⇒x>1/2
x-3>0⇒x>3
2x-1≤x-3
2x-x≤-3+1
x≤-2
нет решения
3)x>0
(1+lgx)²-lgx≥3
lgx=a
(1+a)²-a-3≥0
1+2a+a²-a-3≥0
a²+a-2≥0
a1+a2=-1 U a1*a2=-2⇒a1=-2 U a2=1
a≤-2⇒lgx≤-2⇒x≤0,01 U a≥1⇒lgx≥1⇒x≥10
Ответ x∈(0;0,01] U [10;∞)
a)x∈(0;1)
2x+3>x²⇒x²-2x-3<0
x1+x2=2 U x1*x2=-3⇒x1=-1 U x2=3
-1<x<3 U x∈(0;1)⇒x∈(0;1)
b)x∈(1;∞)
2x+3<x²⇒x²-2x-3>0
x1+x2=2 U x1*x2=-3⇒x1=-1 U x2=3
x<-1 U x>3 U x∈(1;∞)⇒x∈(3;∞)ответ x∈(0;1) U (3;∞)
2)2x-1>0⇒2x>1⇒x>1/2
x-3>0⇒x>3
2x-1≤x-3
2x-x≤-3+1
x≤-2
нет решения
3)x>0
(1+lgx)²-lgx≥3
lgx=a
(1+a)²-a-3≥0
1+2a+a²-a-3≥0
a²+a-2≥0
a1+a2=-1 U a1*a2=-2⇒a1=-2 U a2=1
a≤-2⇒lgx≤-2⇒x≤0,01 U a≥1⇒lgx≥1⇒x≥10
Ответ x∈(0;0,01] U [10;∞)
Приложения:

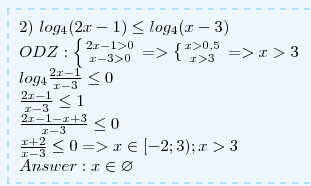


Похожие вопросы
Предмет: Информатика,
автор: Rachermen
Предмет: Биология,
автор: kiexoc
Предмет: Другие предметы,
автор: abdulohmamtov
Предмет: Алгебра,
автор: dashula1907