Предмет: Алгебра,
автор: romashka9
1.ррешить уравнение (смотрите рисунок)
2.докажите что при любом значении а верно неравенство :
(а-5)² > а(а-10) и а²+12 ≥ 4(2а-1)
Приложения:
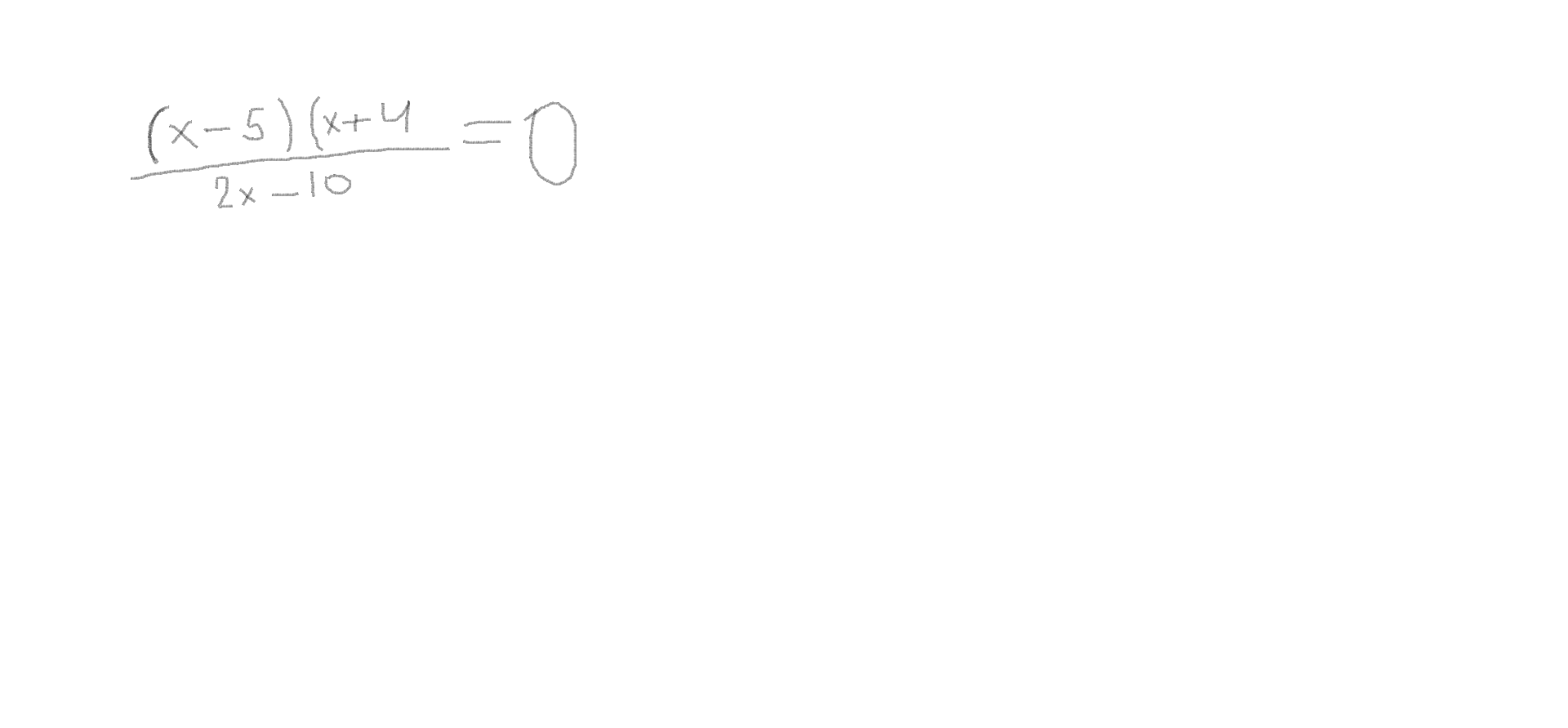
Ответы
Автор ответа:
0
1) (x-5)(x+4)/2(x-5) = 0 одз : х не=5
x+42 = 0
x = -4
2) a2 - 10a +25 - (a2 -10a) > 0
a2 -10a +25 -a2 +10a > 0
25 > 0 при любом а
a2 +12 -4(2a-1) >=0
a2 +12 - 8a +4 >=0
a2 - 8a +16 >=0
(a-4)^2 >= 0 при любом a, т.к. t^2 >=0 ВСЕГДА по свойству арифметического квадрата
Похожие вопросы
Предмет: Физика,
автор: Nami4sama
Предмет: Обществознание,
автор: eva30691
Предмет: География,
автор: jana0797
Предмет: Алгебра,
автор: xkniazx