Предмет: Алгебра,
автор: popikov
чему равна площадь фигуры ограниченной линиями y=(3x+2)(x-1) .y=0
Ответы
Автор ответа:
0
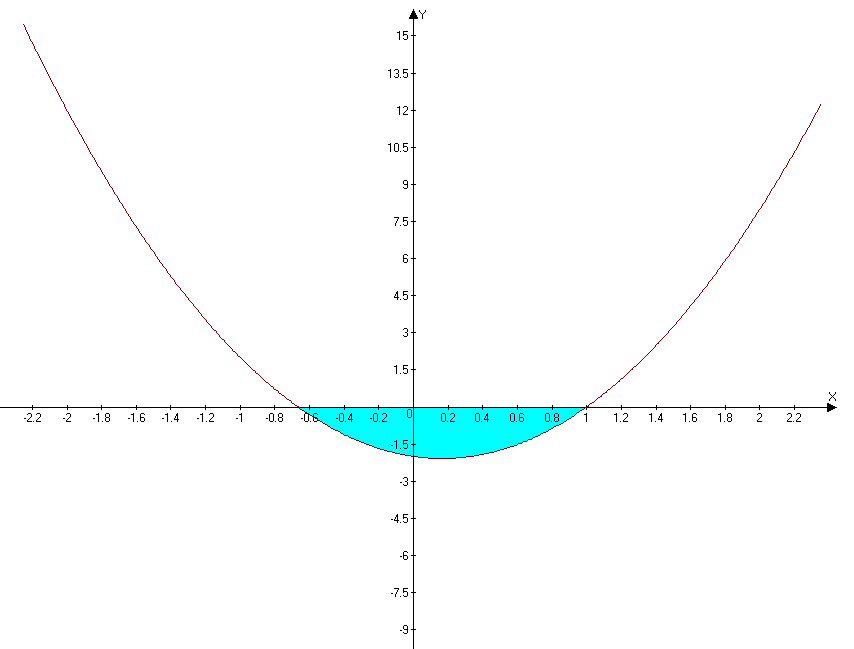
Я так понимаю нужно через интеграл решать
Вначале найти корни уравнения
(3x+2)(x-1)=0
Приложения:
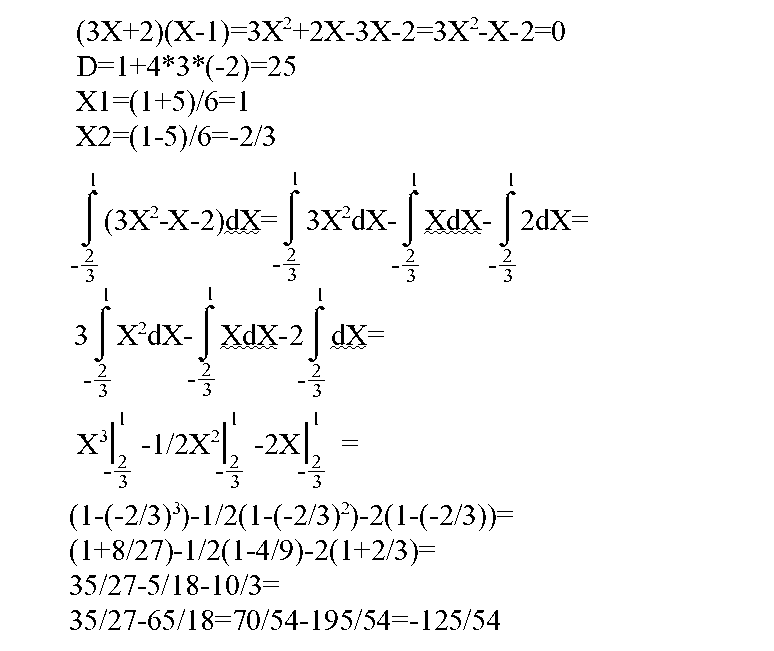
Автор ответа:
0
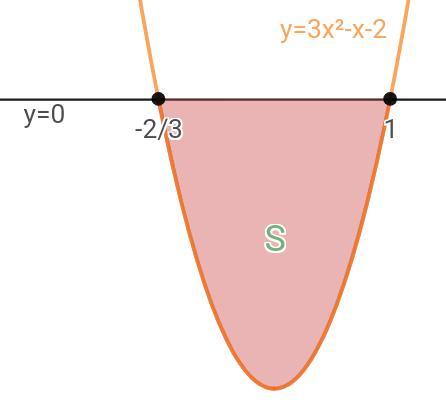
y=(3x+2)(x-1)=3x²-x-2
Это парабола, ветви направлены вверх т.к. старший коэффициент больше нуля. Нули функции:
у=0 это прямая, которая совпадает с ось Ох.
Получается, что
Ответ:
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: vladislav492
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: atoleubai
Предмет: Математика,
автор: malceva
Предмет: Алгебра,
автор: LenaT