Question

Биссектрису тупого угла параллелограмма делит противоположную сторону в отношении 3:4
считая от вершины тупого угла . найдите большую сторону паролелограма, если его периметр равен 88

Answer 1

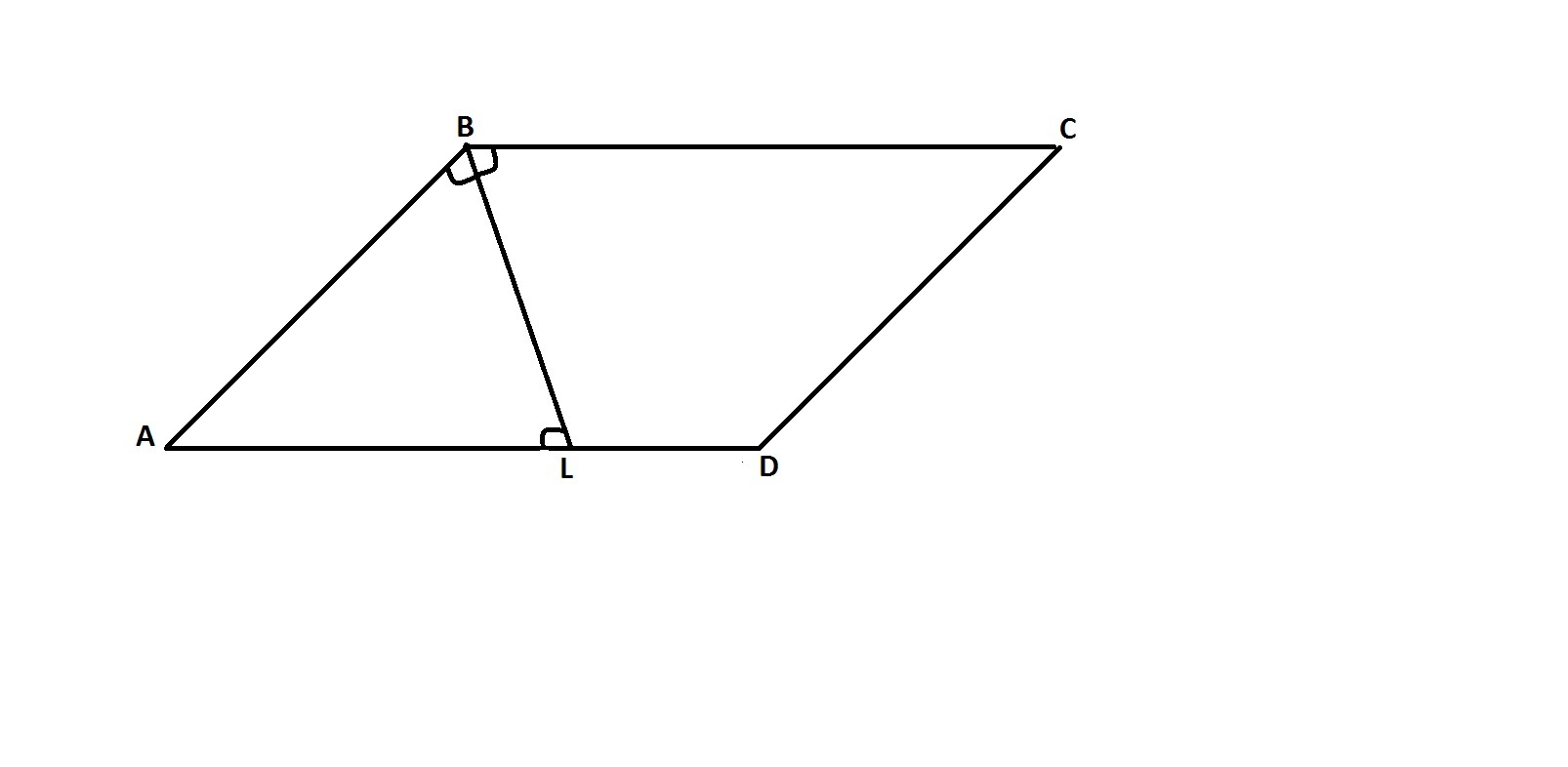
Пусть BL - данная биссектриса.
∠ABL = ∠LBC - по условию;
∠ALB = ∠LBC - как накрест лежащие;
Значит, ∠ALB = ∠ABL. Тогда ΔABL - равнобедренный ⇒ AB = AL.
Пусть $AD = x.$
Тогда $AL = dfrac{4}{7}x and LD = dfrac{3}{7}x$
Тогда и $AB = CD = dfrac{4}{7} x$
Зная, что P = 88, составим уравнение:
$x + x + dfrac{4}{7}x + dfrac{4}{7} x = 88 \ \ 2x + dfrac{8}{7} x = 88 \ \ dfrac{22}{7} x = 88 \ \ x = 28$
Найденная сторона будет большей.
Ответ: 28.