Question

Через произвольную точку основания равнобедренного треугольника проведены прямые, параллельные боковым сторонам треугольника. Докажите, что периметр образовавшегося четырехугольника равен сумме боковых сторон данного треугольника.

Answer 1

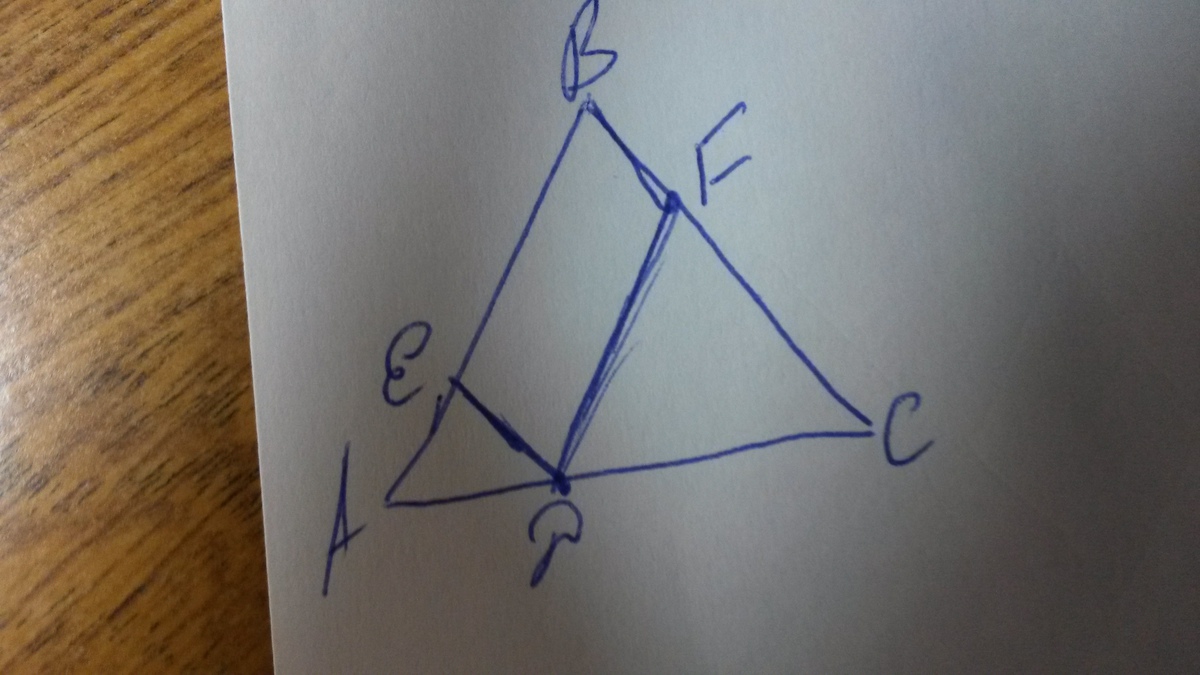
EBFD - параллелограмм, т.к. ED параллельна BF, а EB параллельна FD. Отсюда следует, что ED=BF, EB=DF.
AE=BF, EB=FC. Значит АВ+ВС=BE+BF+FD+DE. ч.т..д.