Предмет: Алгебра,
автор: Давид98
Найти предел, Lim (x-->+бесконечность) (9*x^2+1)^(1/2)-3*x
Только с решением! Иначе смысла нету!
Приложения:
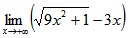
Ответы
Автор ответа:
0
При х-->+бесконечность подкоренное выражение -->3х. 3х-3х =0.
Автор ответа:
0
не совсем ясно, если учесть, что я еще не проходил пределы)
Автор ответа:
0
Приложения:
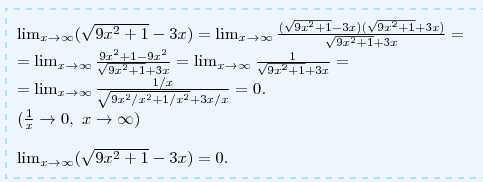
Похожие вопросы
Предмет: Другие предметы,
автор: dimadigma2008
Предмет: Алгебра,
автор: felixleonor2007
Предмет: Алгебра,
автор: wwww2508
Предмет: Химия,
автор: marina9010
Предмет: Математика,
автор: alinkakalinka1