Question

на координатной плоскости покажите штриховкой множество точек заданных системой неравенств
x^2+y^2<=0,64
y>=0

Answer 1

x²+y²=0,64 - уравнение окружности с центром в точке (0;0)
и радиусом 0,8
R²=0,64  ⇒   R=0,8

Неравенству  x²+y²≤0,64 удовлетворяют точки внутри окружности.
Для этого достаточно взять любую из таких точек, например (0;0) и подставить ее координаты в неравенство
0²+0²≤0,64  -  верно.

у=0 - уравнение прямой, эта прямая ось Ох.
Она разбивает координатную плоскость на две части: верхнюю и нижнюю.
Неравенству  у≥0 удовлетворяют точки верхней полуплоскости
Например, точки (1;1) и (2;2) вторая координата больше или равна 0

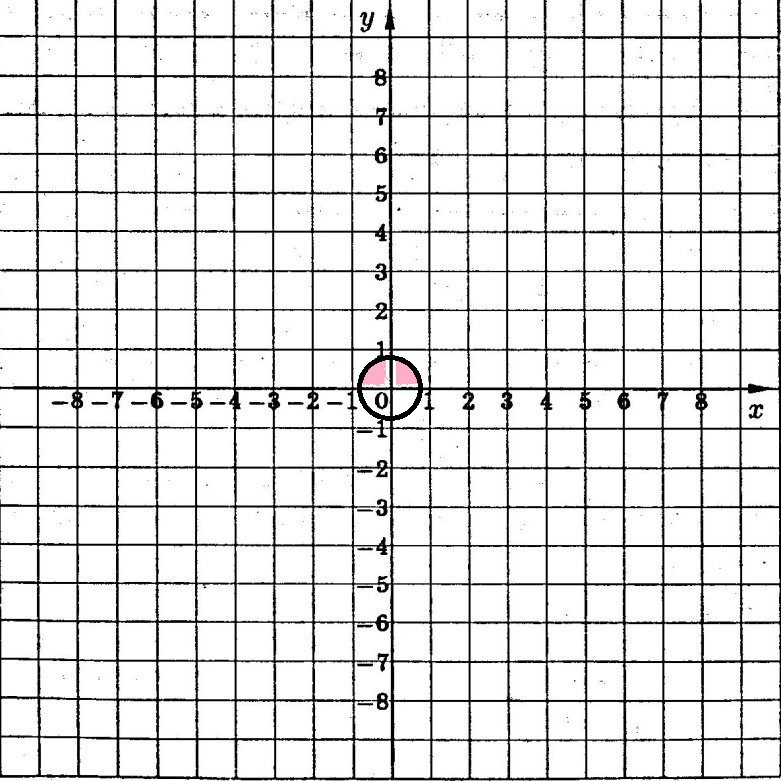
Системе неравенств соответствует пересечение двух областей - внутренность круга, расположенная выше оси ох.