Предмет: Геометрия,
автор: poporo
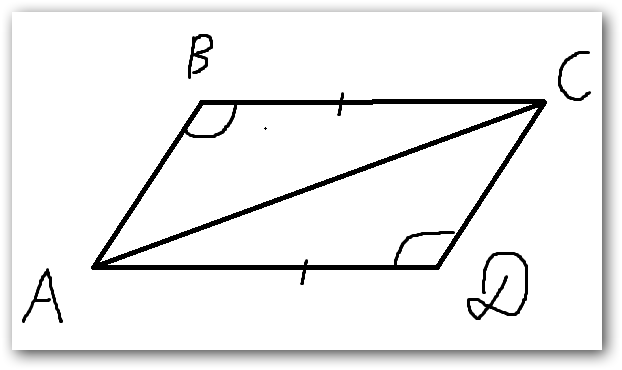
Доказать, что ΔАВС=ΔАDС
Приложения:
Ответы
Автор ответа:
0
По теореме косинусов в треугольнике АВС: АС²=АВ²+ВС²-2*АВ*ВС*CosB (1)
По теореме косинусов в треугольнике АDС: АС²=DC²+AD²-2*DC*AD*CosD (2).
Но <B=<D, а ВС=AD (дано). Приравняем (1) и (2):
АВ²+ВС²-2*АВ*ВС*CosB = DC²+ВС²-2*DC*ВС*CosВ. Это равенство возможно только при равенстве АВ и DC. Тогда треугольники АВС и ADC равны по второму признаку равенства треугольников - по двум сторонам и углу между ними.
Что и требовалось доказать.
По теореме косинусов в треугольнике АDС: АС²=DC²+AD²-2*DC*AD*CosD (2).
Но <B=<D, а ВС=AD (дано). Приравняем (1) и (2):
АВ²+ВС²-2*АВ*ВС*CosB = DC²+ВС²-2*DC*ВС*CosВ. Это равенство возможно только при равенстве АВ и DC. Тогда треугольники АВС и ADC равны по второму признаку равенства треугольников - по двум сторонам и углу между ними.
Что и требовалось доказать.
Автор ответа:
0
Верно. В архив
Похожие вопросы
Предмет: Алгебра,
автор: ykeppusu7048
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: fastkillkoll
Предмет: Математика,
автор: latleha
Предмет: Алгебра,
автор: dasharomch200