Предмет: Алгебра,
автор: marliya111
Помогите пожалуйста решить,ОООЧЕНЬ НАДО
с 106 по 115 номера
Нужно выразить производную
Пожалуйстаааа
Приложения:
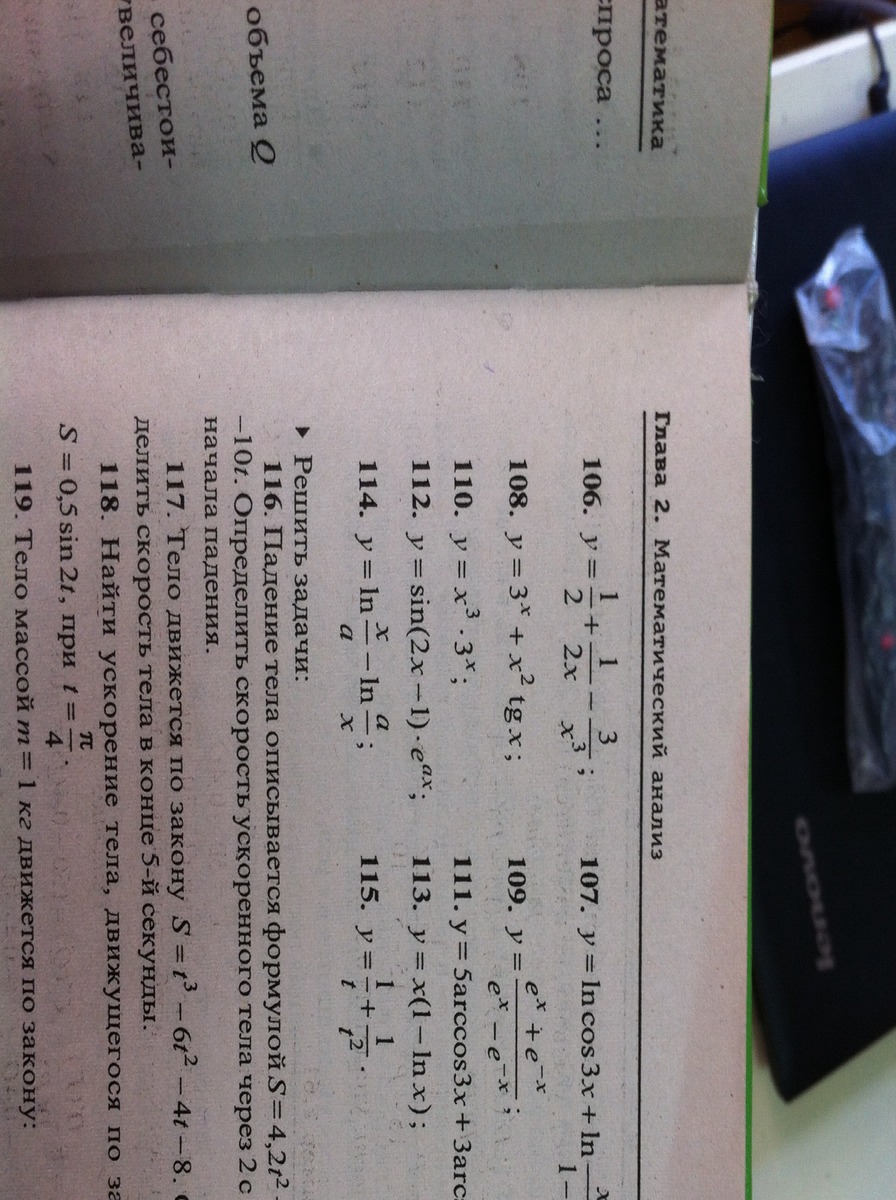
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Обществознание,
автор: nina993
Предмет: Физика,
автор: elbekmamadiev2007
Предмет: Математика,
автор: csgofastt02
Предмет: Обществознание,
автор: alenady