Предмет: Геометрия,
автор: partner88
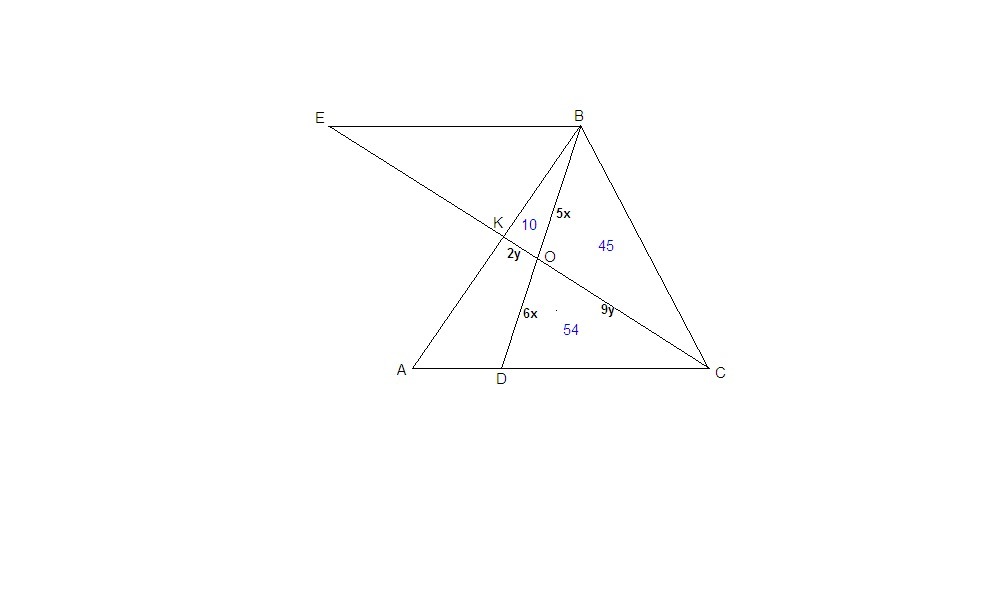
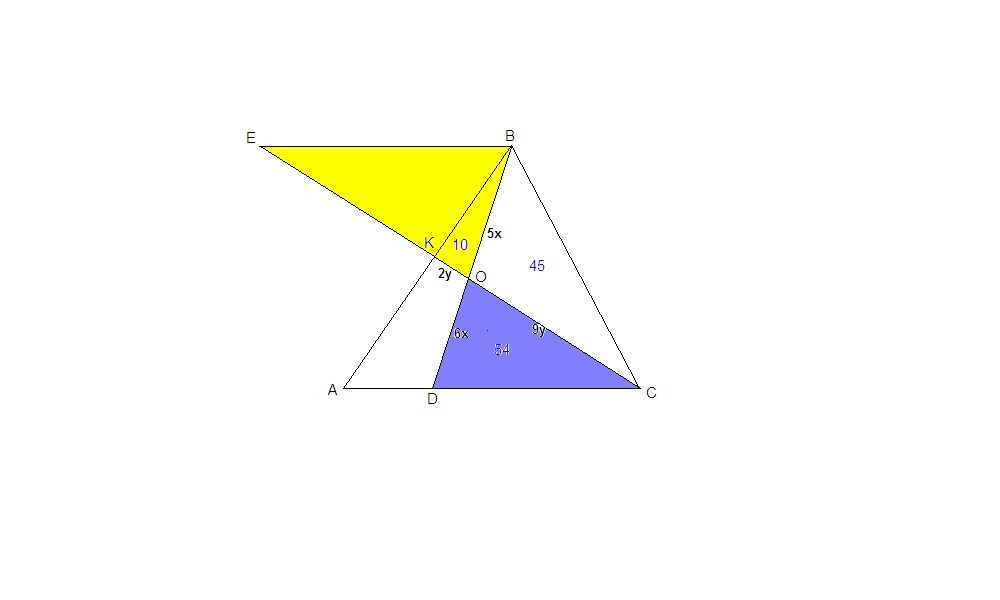
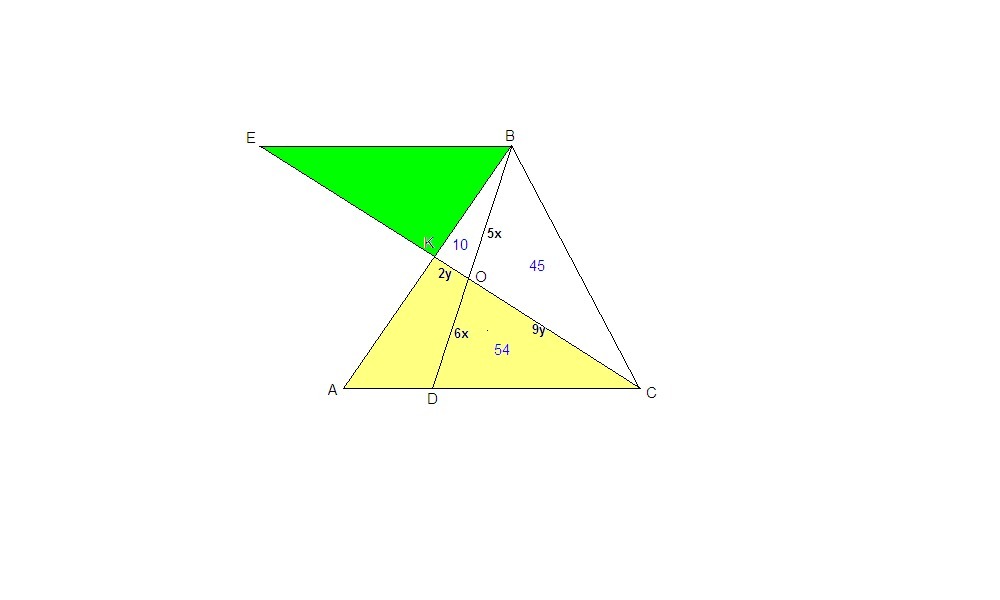
Точка K лежит на стороне AB треугольника ABC, точка D - на стороне AC, прямые BD и CK пересекаются в точке O. Площади треугольников OKB, OBC, OCD соответственно равны 10, 45, 54. Найти площадь треугольника ABC.
Ответы
Автор ответа:
0
В решении используется свойство треугольников, имеющих общую высоту: площади треугольников, имеющих общую высоту относятся как основания, к которым проведена эта высота.
Сами общие высоты на рисунках не проведены.
ΔВОК и ΔВОС имеют общую высоту (из вершины В):
Sbok : Sboc = OK : OC = 10 : 45 = 2 : 9
ΔСОВ и ΔCOD имеют общую высоту (из вершины С):
Scob : Scod = BO : OD = 45 : 54 = 5 : 6
Проведем ВЕ║АС до пересечения с прямой СК.
.
ΔЕВО подобен ΔСВО по двум углам:
ЕО : ОС = ВО : OD
EO = (OC · BO) / OD
EO = (5x · 9y) / (6x ) = 45y / 6 = 15y /2
EK = EO - KO = 15y / 2 - 2y = 11y / 2
ΔEBK подобен ΔСАК по двум углам:
ВК : КА = ЕК : КС = (11y/2) : (11y) = 1 : 2
ΔCBK и ΔСАК имеют общую высоту (из вершины С):
Scbk : Scak = BK : KA = 1 : 2
Scak = 2 · Scbk = 2 · 55 = 110
Sabc = Scbk + Scak = 55 + 110 = 165
Сами общие высоты на рисунках не проведены.
ΔВОК и ΔВОС имеют общую высоту (из вершины В):
Sbok : Sboc = OK : OC = 10 : 45 = 2 : 9
ΔСОВ и ΔCOD имеют общую высоту (из вершины С):
Scob : Scod = BO : OD = 45 : 54 = 5 : 6
Проведем ВЕ║АС до пересечения с прямой СК.
.
ΔЕВО подобен ΔСВО по двум углам:
ЕО : ОС = ВО : OD
EO = (OC · BO) / OD
EO = (5x · 9y) / (6x ) = 45y / 6 = 15y /2
EK = EO - KO = 15y / 2 - 2y = 11y / 2
ΔEBK подобен ΔСАК по двум углам:
ВК : КА = ЕК : КС = (11y/2) : (11y) = 1 : 2
ΔCBK и ΔСАК имеют общую высоту (из вершины С):
Scbk : Scak = BK : KA = 1 : 2
Scak = 2 · Scbk = 2 · 55 = 110
Sabc = Scbk + Scak = 55 + 110 = 165
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sladkyilimonchik
Предмет: Математика,
автор: zamirazzzz123
Предмет: ОБЖ,
автор: pirozochek1337
Предмет: Информатика,
автор: kravcova97
Предмет: Математика,
автор: qaws1990