Question

Решите, пожалуйста, задачу. С рисунком и решением.
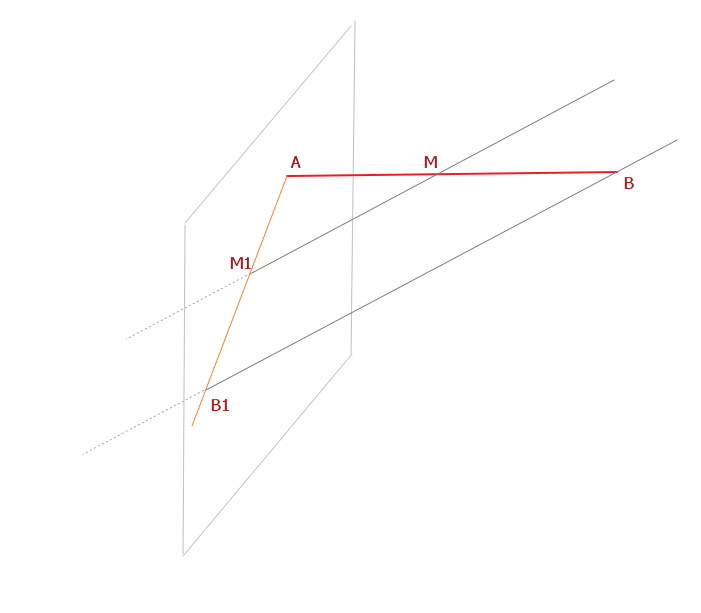
Через конец A отрезка AB проведена плоскость альфа. Через точку M-середину отрезка AB- и точку B проведены параллельные прямые, пересекающие плоскость альфа в точках M1 и B1 соответственно.
а) Докажите, что точки A, B1, M1 лежат на одной прямой.
б) Найдите BB1, если MM1=4 см.

Answer 1

точки А и М лежат на одной прямой,
точка М1 по условию лежит в плоскости альфа...
через эти три точки можно провести плоскость (АММ1), которая будет пересекаться с плоскостью альфа, т.к. по условию для этих плоскостей точка М1 --общая...
пересечение двух плоскостей ---это прямая линия)))
точи А и М1 принадлежат по условию и плоскости альфа, и плоскости (АММ1), следовательно эти точки лежат на прямой, которая является пересечением этих плоскостей...
про В1 аналогично... В1 тоже принадлежит плоскости (АММ1)
получили треугольник АВВ1, в нем ММ1 -- средняя линия...
следовательно, ВВ1 = 4*2 = 8