Question

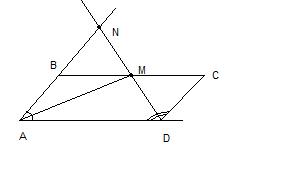
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке M,лежащей на стороне BC. Луч DM пересекает прямую AB в точке N.Найдите периметр параллелограмма ABCD, если AN=10см.

Answer 1

<BMA=<DAM как накрест лежащие углы при пересечении двух параллельных прямых AD и ВС секущей АМ. Но 
< DAM=<BAM, т.к. АМ - биссектриса, значит 
<BMA=<BAM, и треуг-ик АВМ равнобедренный (т.к. углы при его основании АМ равны). Значит АВ=ВМ.
<CMD=<ADM как накрест лежащие углы при пересечении двух параллельных прямых AD и ВС  секущей DM. Но 
<ADM=CDM, т.к. DM - биссектриса, значит 
<CMD=<CDM, и треуг-ик DCM также равнобедренный (углы при его основании DM равны). Т.е.
АВ=CD=BM=CM
Пусть АВ будет х (соответственно, CD, BM и СМ также будут х). Зная, что AN=10, запишем:
АВ=AN-BN, BN=AN-AB=10-x
Рассмотрим треуг-ки BNM и CDM. Они равны по второму признаку равенства: сторона и два прилежащих к ней угла одного треуг-ка соответственно равны стороне и двум прилежащим к ней углам другого треуг-ка. В нашем случае:
- ВМ=СМ;
- <BMN=<CMD как вертикальные углы;
- <MBN=<MCD как накрест лежащие углы при пересечении двух параллельных прямых AN и CD секущей ВС. Значит
BN=CD=x
Выше выведено, что BN=10-x. Приравняем 10-х и х, раз речь идет об одном и том же:
10-х=х
2х=10
х=5
АВ=CD=5 см, AD=BC=5+5=10 см
Р ABCD = 2AB+2BC=2*5+2*10=30 см