Question

Помогите решить задачу, пожалуйста, если можно с описанием
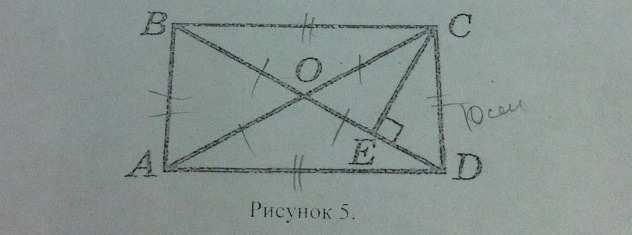
АВСD - прямоугольник, СЕ перпендикулярна к ВD, CD = 10 см, DE : OC = 1 : 2
Найдите диагонали прямоугольника

Answer 1

Рассмотрим треуг-ик COD. Здесь СО=DO, т.к. диагонали прямоугольника равны и делятся точкой пересечения пополам. Т.е. COD - равнобедренный с основанием CD. Поскольку DE : OC = 1 : 2, мы можем записать, что DE : DO = 1 : 2, т.е. Е - середина стороны DO.
Если принять OD за основание треуг-ка COD, мы видим, что СЕ - его высота и медиана одновременно. Если в треугольнике высота является медианой, то этот треугольник равнобедренный. Значит,
СО=CD. Но СО=DO, значит СО=СD=DO, и треуг-ик COD - равносторонний.
СО=СD=DO=10 см,
АС=BD=2*CO=2*10=20 см

Answer 2

спасибо!