Question

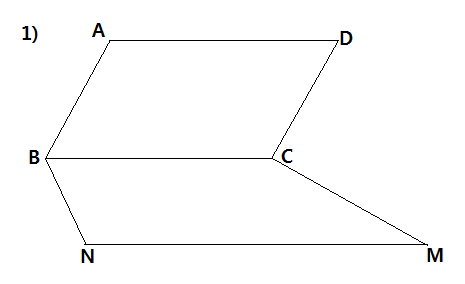
1) Ромб ABCD и трапеция BCMN ( BC - ее основа ) не лежат на одной плоскости . Как размещены прямые MN и AD? Объяснить.
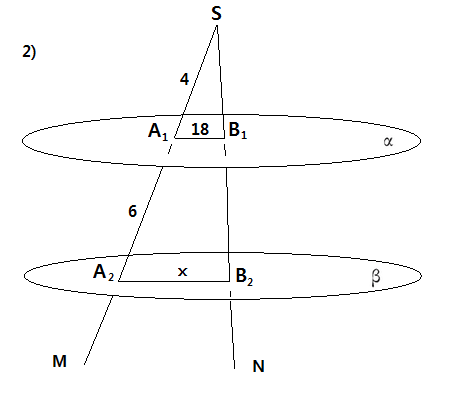
2) Сторона SM угла S пересекает параллельные плоскости альфа и бета в точках A1 и А2, а сторона SN - в точках B1 и B2 соответственно. Найти длину отрезка A2B2 если A1B2 = 18 cм, SA1 =4 cм, A1A2 = 6 cм.

Answer 1

Рисунки к задачам смотри в прикрепленных файлах.

1) Так как ABCD - ромб, то его противоположные стороны параллельны: AD || DC; 
BCMN - трапеция, следовательно основы DC || NM параллельны
Из 2х утверждений выше следуя теореме про транзитивность прямых (если две прямые параллельны третьей, то эти две прямые между собой тоже параллельны) => AD || DC 

2) Так как α || β, то А1В1 || A2B2 (через SN и SM лучи, которые пересекаются, можно провести плоскость, и при том только одну; сл-но плоскость, которая пересекает 2 параллельные плоскости будет пересекать их по параллельным прямым, а у нас А1В1 и A2B2 будут на них лежать, сл-но и отрезки, которые лежать на параллельных прямых, тоже будут параллельны).

ΔA1SB1~ΔA2SB2 по 3ему признаку (по 3м углам), значит выполняется следующее соотношение:
$frac{A_1S}{A_2S} = frac{A_1B_1}{A_2B_2} \ frac{4}{10} = frac{18}{x} \ 4x=180 \ x=45 - A_2B_2$