Question

При каких значениях параметра a уравнение ∣x−1∣=ax+1 имеет два решения?

Answer 1

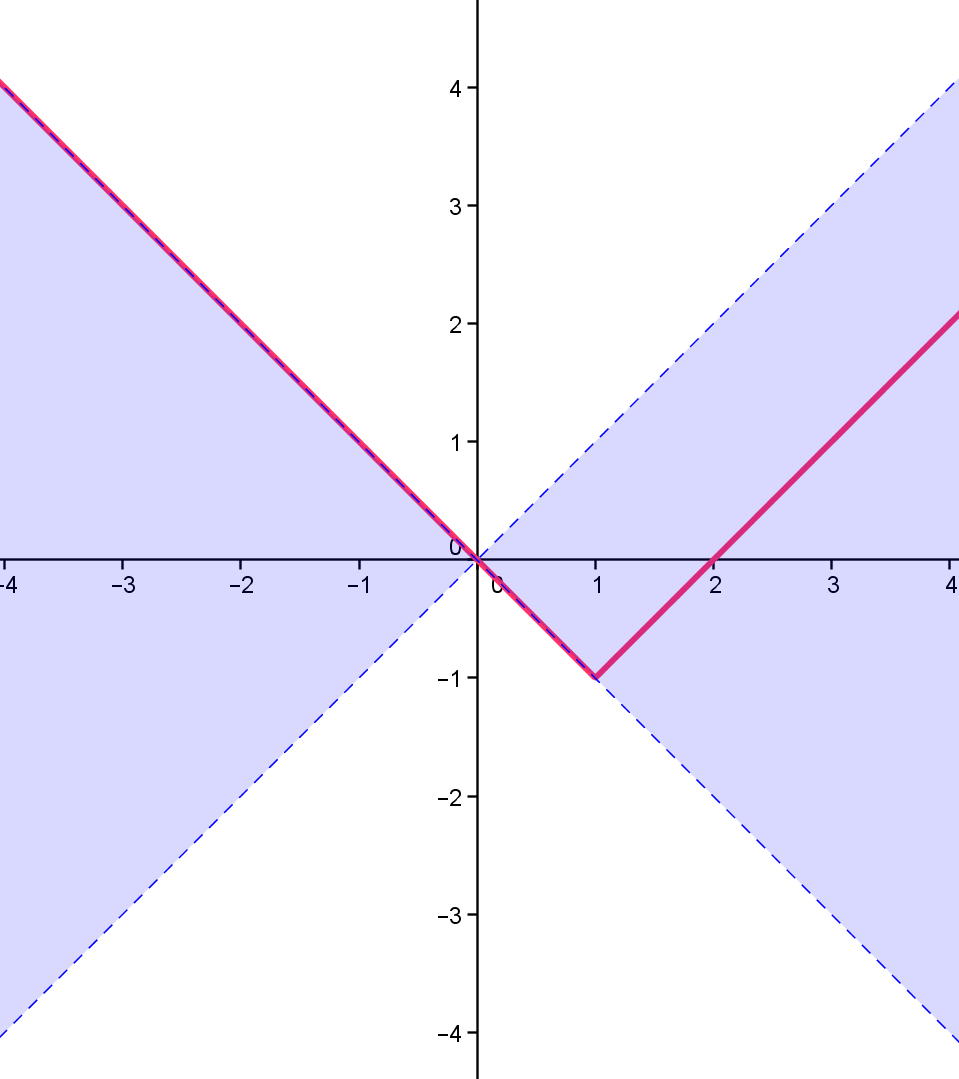
Будем решать графически. На рисунке красным выделен график функции y = |x - 1| - 1.
Необходимо понять, при каких a прямая y = ax будет иметь с графиком ровно две точки пересечения.

Понятно, что одна точка пересечения будет всегда- это точка (0, 0).  Так как y = ax - прямая, проходящая через начало координат, то шансов получить еще ровно одну точку пересечения с графиком левее x = 1 шансов нет. Тогда должна быть точка пересечения правее x = 1.

Утверждаю, что такое может случиться, если и только если прямая будет проходить через закрашенную область, т.е. при -1 < a < 1.