Question

Площадь прямоугольного треугольника равна578 корней из 3 делённое на 3. Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.

Answer 1

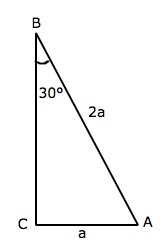
Обозначим треугольник АВС, С=90°, В=30°

Пусть АС=а, тогда гипотенуза AB= а:sin30°=2a.

∠А=90°-30°=60°

Площадь треугольника равна половине произведения сторон, умноженного на синус угла между ними. 

S=AB•AC•sin60°:2

578√3/3=(a•2a•√3/2):2=a²√3/2

a²=(289•2√3:3):(√3/2)=289•4/3

a=17•2/√3=34/√3

BC=AC•tg60°=(34/√3)•√3=34

Проверка:

S=a•b:2

S=34•34/√3):2=578/√3=578√3/3