Question

Круговой сектор ограничен радиусами, равными 5см, и дугой в 90°. Найдите площадь круга, вписанного в этот сектор.

Answer 1

Центр вписанной в угол окружности лежит на его биссектрисе.
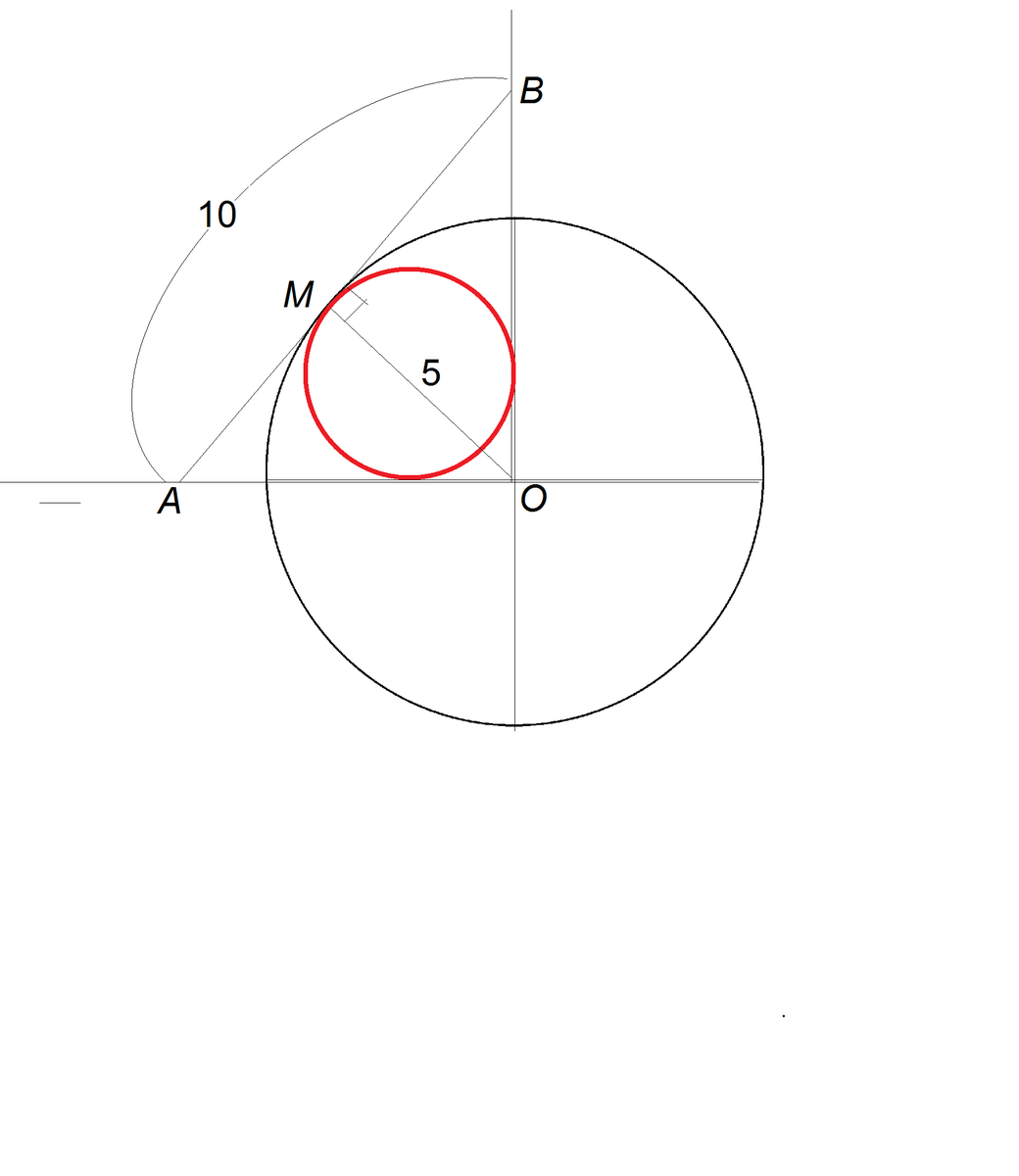
Вписанная в сектор окружность касается  дуги сектора в точке пересечения биссектрисы с дугой сектора - в точке М.
Проведем радиус ОМ в эту точку.
К точке М проведем касательную АВ до пересечения с продолжениями сторон сектора.
Треугольник АОВ - равнобедренный, т.к. углы А и В равны 45° ( из треугольников АМО и ВМО)
Окружность, вписанная в сектор, вписана также в равнобедренный прямоугольный треугольник, в котором радиус сектора является медианой. ⇒АВ=10, АМ=МВ=5, 
АО=ОВ=5√2 по свойству гипотенузы равнобедренного прямоугольного треугольника.
Радиус вписанной в прямоугольный треугольник окружности находят по формуле:
r=(a+b-c):2
r=(10√2 -10):2=5(√2 -1)
Площадь круга 
S=πr²=5²(√2 -1)²
S=25π (3-2√2) и это примерно 4,29π см² или ≈13,475 см²

Answer 2

в конце 3 - 2 корня из двух = корень из 9 - 8 = 1

Answer 3

Следовательно, площадь=25пи

Answer 4

25π это площадь всего круга радиусом 5 см, из которого выделен сектор, а не круг, вписанного в сектор. Площадь окружности 25π*(3-2√2). Да и устно можно прикинуть, что если в сектор, занимающий 1/4 круга, вписать круг, то его площадь будет меньше площади исходного круга с радиусом 5 см.

Answer 5

(3-2√2)=0,17( примерно) Умножив на 25 получим 4, 29 и затем на π ( я на калькуляторе умножила, нажав π, а не на 3,14) Вот и получилось данное в ответе число.

Answer 6

. Площадь не окружности, а круга, конеччно.