Question

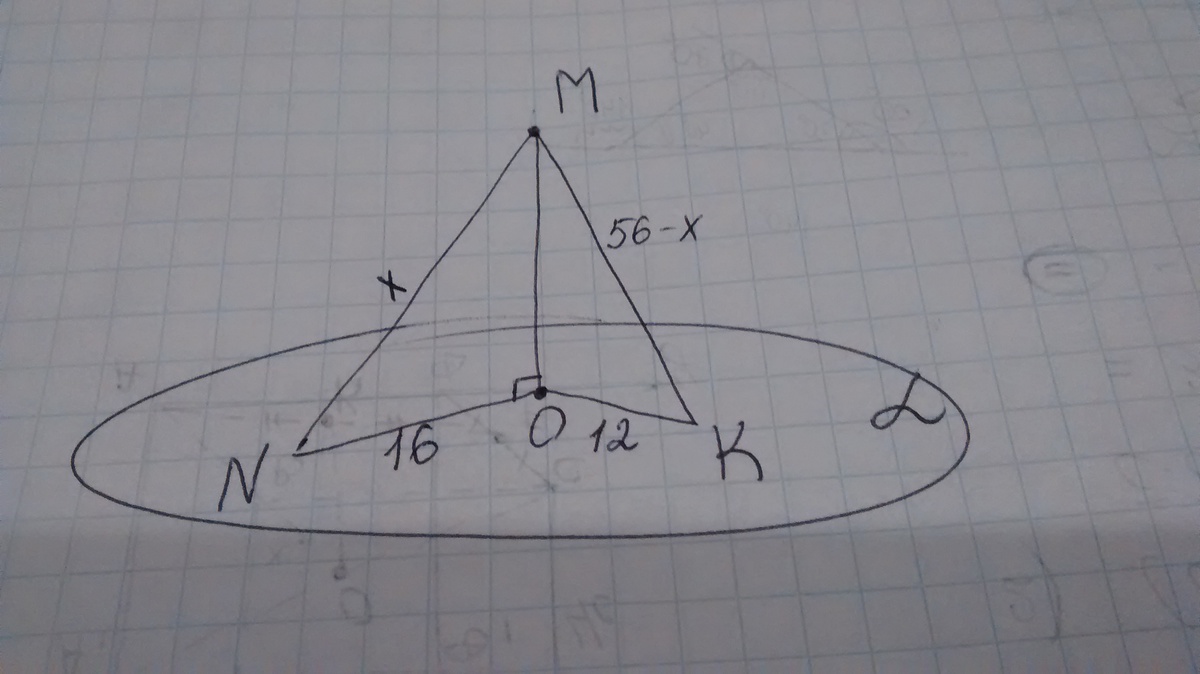
З точки, яка не належить площині, проведено до неї дві похилі, довжини проекцій яких дорівнюють 12 см і 16 см, а сума довжин похилих — 56 см. Знайдіть довжини похилих.

Answer 1

Рисунок до задачі див. у прикріпленому файлі.

Нехай $MO$ - перпендикуляр до площини α, $MK, MN$ - похилі, а $NO, OK$ - проекції цих похилих на площину.

Δ$MOK$ і Δ$MON$ - прямокутні.
$MO$ - спільний перпендикуляр, спільний катет у цих двох трикутниках. Виразимо за теоремою Піфагора його з кожного трикутника та прирівняємо.

$NO=16;OK=12; \ MN=x;MK=56-x; \ MO^2=MN^2-NO^2=x^2-16^2 \ MO^2=MK^2-OK^2=(56-x)^2-12^2 \ x^2-16^2=(56-x)^2-12^2 \ x^{2} -256=3136-112x+ x^{2} -144 \ 112x=3136-144+256 \ 112x=3248 \ x=29-NM \ MK=56-29=27$