Предмет: Алгебра,
автор: agasikkk
Задание внутри.Пример легкий
Приложения:
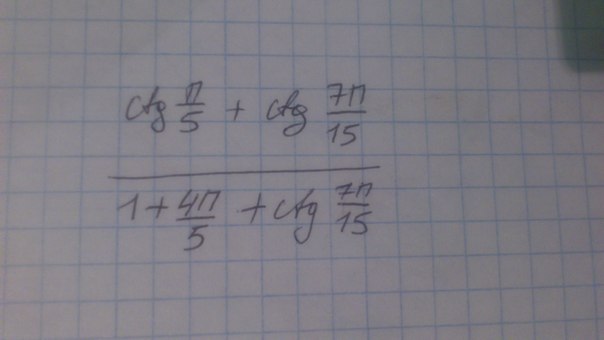
Ответы
Автор ответа:
0
сtgπ/5+ctg7π/15=(cosπ/5sin7π/15+sinπ/5cos7π/15)/sinπ/5sin7π/15=
=sin(2π/3)/sinπ/5sin7π/15=sin(π/3)/sinπ/5sin7π/15
1+ctg4π/5*ctg7π/15=(sin4π/5sin7π/15+cos4π/5cos7π/15)/sin4π/5sin7π/15=
=cos(π/3)/sin4π/5sin7π/15=cos(π/3)/sinπ/5sin7π/15
(сtgπ/5+ctg7π/15)/(1+ctg4π/5*ctg7π/15)=
=sin(π/3)/sinπ/5sin7π/15 :cos(π/3)/sin4π/5sin7π/15=
=sin(π/3)/sinπ/5sin7π/15*sinπ/5sin7π/15/cosπ/3=sin(π/3)/cos(π/3)=tg(π/3)=√3
=sin(2π/3)/sinπ/5sin7π/15=sin(π/3)/sinπ/5sin7π/15
1+ctg4π/5*ctg7π/15=(sin4π/5sin7π/15+cos4π/5cos7π/15)/sin4π/5sin7π/15=
=cos(π/3)/sin4π/5sin7π/15=cos(π/3)/sinπ/5sin7π/15
(сtgπ/5+ctg7π/15)/(1+ctg4π/5*ctg7π/15)=
=sin(π/3)/sinπ/5sin7π/15 :cos(π/3)/sin4π/5sin7π/15=
=sin(π/3)/sinπ/5sin7π/15*sinπ/5sin7π/15/cosπ/3=sin(π/3)/cos(π/3)=tg(π/3)=√3
Похожие вопросы
Предмет: Окружающий мир,
автор: egornick559
Предмет: Информатика,
автор: cherry2137
Предмет: Математика,
автор: DGlare
Предмет: Математика,
автор: супердевочка1
Предмет: Физика,
автор: sallenn