Question

исследуйте (с помощью 2-й производной) на экстремум функцию y=9x^2 +4

Answer 1

$y=9x^2+4$
1) область определения функции
$D(y)=R$ -все действительные числа.
2) Производная функции:
Производная постоянной 4 равна нулю.
Производная произведения константы на функцию есть произведение этой константы  на производную данной функции.
В силу правила, применим: $x^n=nx^{n-1}to x^2=2x^{2-1}=2x$
Выглядит так: 
$y'=(9x^2+4)'=(9x^2)'+(4)'=9cdot2x+0=18x$
3) Производная равна нулю
18x=0
x=0
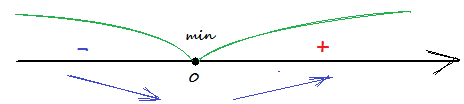
4) Обозначим на промежутке возрастания и убывания производной.
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум (0;4).
Итак, функция возрастает на промежутке $x in (0;+infty)$, убывает - $x in (-infty;0)$ . В т. х = 0 - функция имеем локальный минимум.