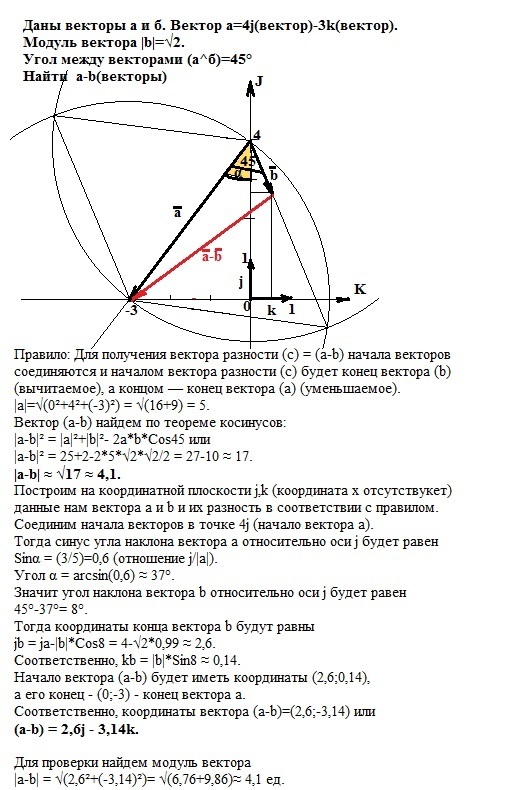
Даны векторы а и б, причемВектор а=4j(вектор)-3k(вектор)
Модуль вектора b=Корень 2
Вектор а^б=45
найти a-b(векторы)
Ответы
Правило: Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Решение.
Для начала найдем модуль вектора а.
Дано разложение вектора по ортам: a=4i-3k, то есть координаты вектора
равны:
X=0 (так как базовый вектор i отсутствует),
Y=4 и Z=-3.
То есть дан вектор а(0;4;-3).
Тогда его модуль равен:
|a|=√(0²+4²+(-3)²) = √(16+9) = 5.
Вектор (a-b) найдем по теореме косинусов:
|a-b|² = |a|²+|b|²- 2a*b*Cos45 или
|a-b|² = 25+2-2*5*√2*√2/2 = 27-10 ≈ 17.
|a-b| ≈ √17 ≈ 4,1.
Мы нашли модуль (длину) вектора разности векторов а и b.
Но можно найти и его разложение по базовым векторам.
Для этого необходимо найти координаты конца вектора b
относительно начала координат.
Построим на координатной плоскости j,k (координата х отсутствукет)
данные нам вектора а и b и их разность в соответствии с правилом.
Соединим начала векторов в точке 4j (начало вектора а).
Тогда синус угла наклона вектора а относительно оси j будет равен
Sinα = (3/5)=0,6 (отношение j/|a|).
Угол α = arcsin(0,6) ≈ 37°.
Значит угол наклона вектора b относительно оси j будет равен
45°-37°= 8°.
Тогда координаты конца вектора b будут равны
jb = ja-|b|*Cos8 = 4-√2*0,99 ≈ 2,6.
Соответственно, kb = |b|*Sin8 ≈ 0,14.
Начало вектора (a-b) будет иметь координаты (2,6;0,14)
а его конец - (0;-3) - конец вектора а.
Соответственно, координаты вектора (a-b)=(2,6;-3,14) или
(a-b) = 2,6j - 3,14k.
Для проверки найдем модуль вектора
|a-b| = √(2,6²+(-3,14)²)= √(6,76+9,86)≈ 4,1 ед.
Это соответствует ранее найденному значению с учетом округлений.