Question

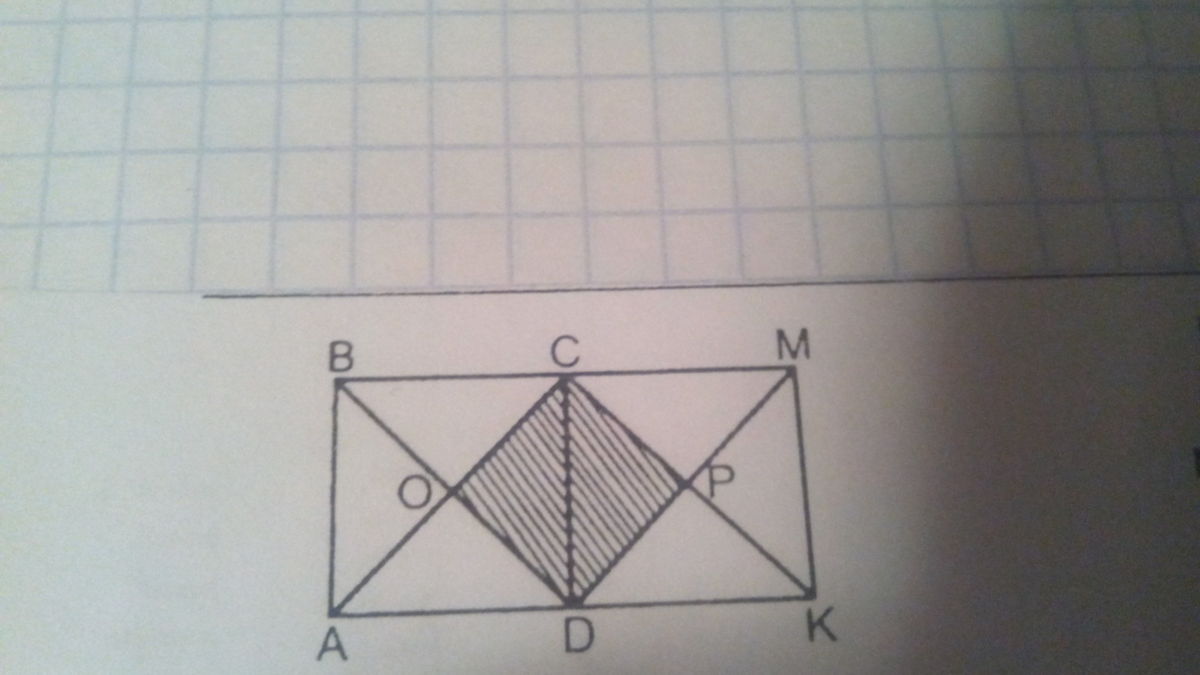
ABCD и DCMK - квадрат AB = 6 см. Найдите площадь и периметр четырехугольника OCPD

Answer 1

Ответ: площадь четырехугольника OCPD равна $18$ см², а периметр - $12sqrt{2}$ см.

Решение:

• Заметим, что OCPD - это квадрат. Большие квадраты ABCD и DCMK между собой равны, так как имеют общую сторону. Диагонали этих квадратов взаимно перпендикулярны (образуют угол 90°) и точкой пересечения делятся пополам. Все стороны четырехугольника OCPD равны половине диагонали большого квадрата, и, поэтому, также равны между собой. А четырехугольник с углами по 90° и равными сторонами является квадратом.

Вначале попробуем найти сторону квадрата OCPD. Как было написано выше, каждая его сторона равна половине диагонали больших квадратов. Сама диагональ равна (по теореме Пифагора):

$displaystyle BD=sqrt{BA^2+AD^2} =sqrt{6^2+6^2} = sqrt{72} = sqrt{36}sqrt{2} = 6sqrt{2}.$

Тогда сторона искомого квадрата равна:

$displaystyle frac{6sqrt{2} }{2} = 3sqrt{2}.$

Теперь можно найти периметр и площадь:

$displaystyle P_square = 4a =4*3sqrt{2} = 12sqrt{2}; cm.\\S_square = a^2 =(3sqrt{2})^2 =3^2sqrt{2} ^2 =9*2=18; cm^2.$      

Answer 2

Ответ:

Объяснение:

OCPD - квадрат со стороной, равной половине диагонали квадрата ABCD, при стороне АВ = 6 см.

Квадраты ABCD и DCMK одинаковы, и они имеют общую сторону. Диагонали этих квадратов взаимно перпендикулярны и точкой пересечения делятся пополам. Все стороны OCPD равны половине диагонали большого квадрата, и, поэтому, также равны между собой. А четырехугольник с прямыми углами и равными сторонами является квадратом.

AC = BD = 6√2 см.

OC = CP = PD = OD = AC/2 = 3√2 см.

Периметр P = 4*3√2 = 12√2 см.

Площадь S = (3√2)^2 = 9*2 = 18 кв.см.