Предмет: Геометрия,
автор: kristinafnikina
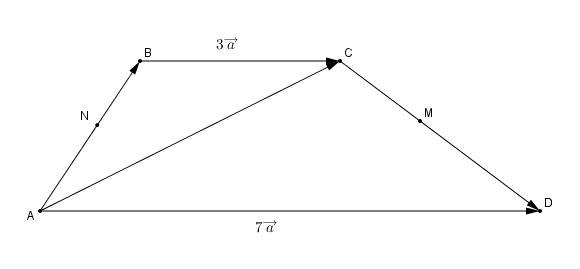
В трапеции ABCD c основаниями BC = 3a и AD = 7a: AN = NB и CM = MD. Найдите величину |AN + BC + MD|.
Ответы
Автор ответа:
0
Рассмотрим треугольники ABC и ACD, по правилу треугольника
Далее сложим эти два равенства
Поскольку N - середина АВ и M - середина CD, то
Следовательно,
Можно еще такой способ. По правилу многоугольника эта сумма равна средней линии , то есть 5а, для наглядности покажу, так как MN средняя линия, то
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Jikalut
Предмет: Алгебра,
автор: sabi0000
Предмет: Биология,
автор: vladimirzudenko1
Предмет: Химия,
автор: Liza9801
Предмет: Математика,
автор: sb2022