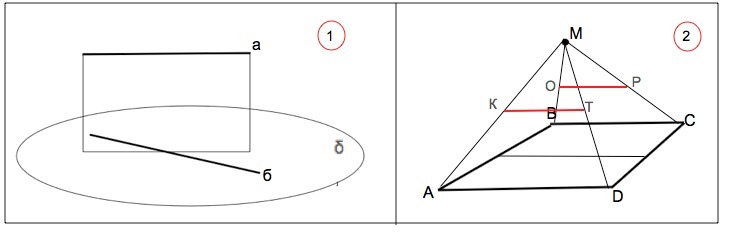
1.Прямая а параллельна плоскости дельта, а прямая б лежит в плоскости дельта.Определите:могут ли прямые а и б : а)пересекаться б) быть скрещивающимися
2.Точка M не лежит в плоскости трапеции ABCD (AD || BC)
Докажите:
а))что треугольники MAD и MBC имеют параллельные средние линии.
б)) найдите длины этих средних линий если AD : BC = 5:3, а средняя линия трапеции равна 16 см
Ответы
Прямая параллельна плоскости, если не имеет с ней общих точек. Прямая а не может пересекаться с прямой б, т.к. в противном случае будет пересекать и плоскость δ.
Прямые а и б могут быть параллельны или быть скрещивающимися.
====
а)Средняя линия ОР треугольника ВМС параллельна ВС ( по определению). ВС параллельна АD по условию. Если одна из двух параллельных прямых параллельна третьей, то они параллельны. ⇒
ОР║ АD
Средняя линия КТ треугольника АМD параллельна AD ⇒ КТ ║ ОР. Доказано.
б) Средняя линия трапеции равна полусумме оснований.⇒
АD+ВС=2•16=32 см
Примем коэффициент отношения оснований трапеции равным х.
Тогда 5х+3х=32 ⇒
8х=32 см
х=4 см
АD=20 ⇒ KT=20:2=10 см
BC=12 ⇒ OP=12:2=6 см