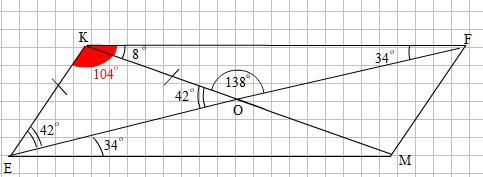
"В параллелограмме EKFM диагонали пересекаются в точке O , причем угол KOF равен 138 градусов ,а угол FEM равен 34 градуса . Найдите угол Kпараллелограмма , если KM в 2 раза больше MF"
Ответы
Ответ:
Объяснение:
рис. во вложении
Диагонали параллелограмма, в точке их пересечения делятся пополам, значит ОК = ОМ = КМ / 2.
По условию, КМ = 2 * FM, отсюда ОМ = FM.
Треугольник ОМF равнобедренный. Угол FOM и FOK смежные углы, значит угол FOM = 180 – 138 = 42°.
Так как треугольник OMF равнобедренный, то угол FOM = OFM = 42°. В треугольнике EFM определим угол EMF.
Угол EMF = 180 – FEM – EFM = 180 – 34 – 42 = 104°. Так как у параллелограмма противоположные углы равны, то угол ЕКF = EMF = 104°.
Угол ЕКF равен 104°.
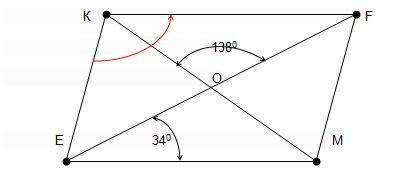
Ответ:
∠K = 104°
Объяснение:
Дано: EKFM - параллелограмм
∠KOF = 138°
∠FEM = 34°
KM = 2 MF
Найти: ∠К
-------------------------------------
Смотри рисунок на прикреплённом фото.
∠KFO = ∠FEM = 34° (внутренние накрест лежащие при параллельных KF и EM и секущей EF.
Тогда в ΔKOF угол FKO = 180° - (138° + 34°) = 8°
∠KOE и ∠ KOF смежные, следовательно ∠KOE = 180° - 138° = 42°
ΔЕКО равнобедренный, так как ЕК = MF как противоположные стороны параллелограмма, а MF = 0.5KM по условию, и KO =0.5KM как половина диагонали, поэтому ЕК = КО.
Тогда ∠КЕО = ∠КОЕ = 42° и ∠ЕКО = 180° - 2 · 42° = 96°
∠К = ∠ЕКО + ∠FKO = 96° + 8° = 104°