Предмет: Алгебра,
автор: 1996sasha
Вычисли площади фигур ограниченных линиями см рис
Построить заданные фигуры
Значения n=29, m=7
Приложения:
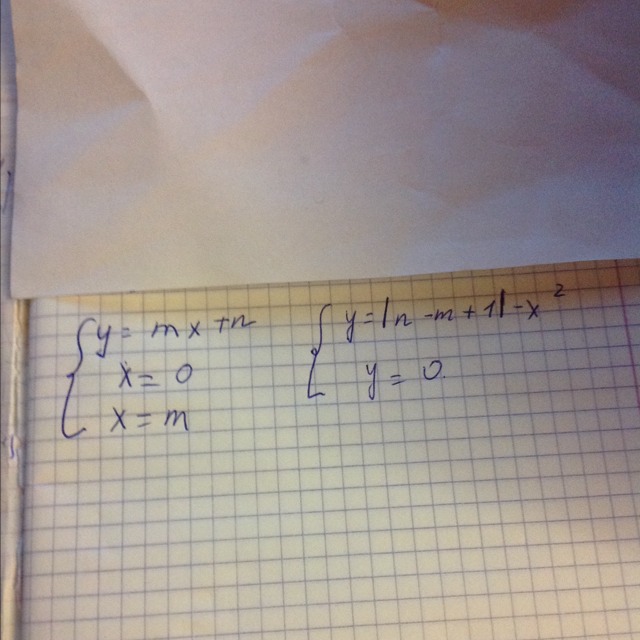
Ответы
Автор ответа:
0
1) у=0 - ось ох
х=7 - прямая || оси оу
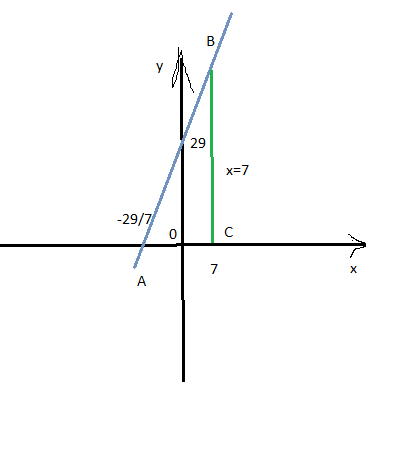
у=7х+29 - прямая пересекающая ось ох в точке (-29/7; 0) и ось оу в точке (0; 29)
Искомая площадь - площадь треугольника АВС
Можно найти как половина произведения катетов
Один катет по оси ох 7 - (-29/7)=78/7
Второй по оси у - ордината прямой у=7х+29 при х=7
у=7·7+29=78

или

2) y=|n-m+1|-x² при n=29, m=7 принимает вид
у=|29-7+1|-x²
или
у=23-х²
Графиком является парабола, ветви которой направлены вниз, парабола имеет вершину в точке (0;23) и пересекает ось ох в точках (-√23; 0) и (√23; 0)
у=0 - уравнение оси ох
Искомая площадь - площадь под параболой, снизу ограничена осью ох


х=7 - прямая || оси оу
у=7х+29 - прямая пересекающая ось ох в точке (-29/7; 0) и ось оу в точке (0; 29)
Искомая площадь - площадь треугольника АВС
Можно найти как половина произведения катетов
Один катет по оси ох 7 - (-29/7)=78/7
Второй по оси у - ордината прямой у=7х+29 при х=7
у=7·7+29=78
или
2) y=|n-m+1|-x² при n=29, m=7 принимает вид
у=|29-7+1|-x²
или
у=23-х²
Графиком является парабола, ветви которой направлены вниз, парабола имеет вершину в точке (0;23) и пересекает ось ох в точках (-√23; 0) и (√23; 0)
у=0 - уравнение оси ох
Искомая площадь - площадь под параболой, снизу ограничена осью ох
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zoya0639
Предмет: Математика,
автор: vladverzun2009
Предмет: Английский язык,
автор: lerysek282828852
Предмет: Алгебра,
автор: эпплджеки
Предмет: Математика,
автор: alenka1607