Question

1)Исследуйте функцию $y= frac{x}{|x|}+x^{3}+x+ x^{2}$ на четность.
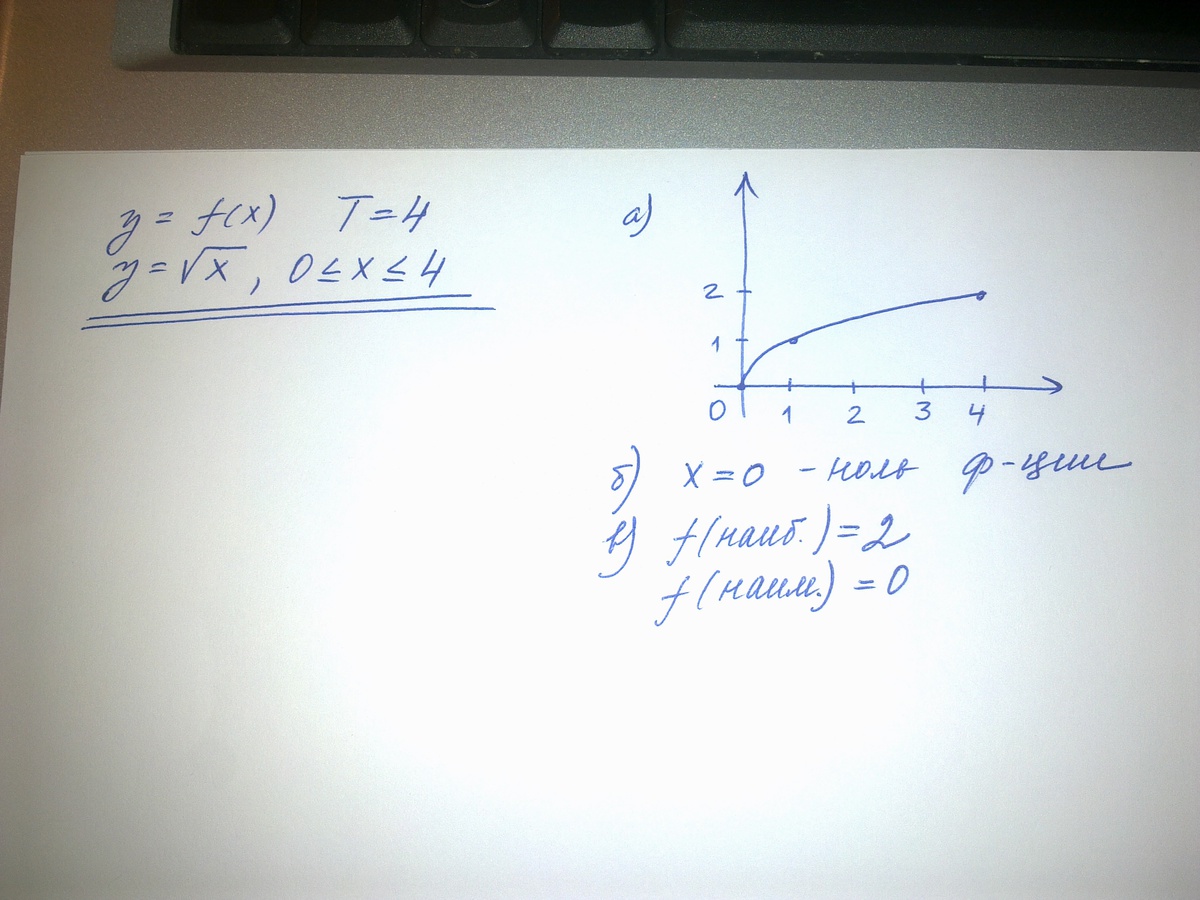
2)y=f(x) - периодическая функция с периодом T=4. Известно, что y=$sqrt{x}$, если 0 $leq x leq 4$.
а)Постройте график функции. 
б)Найдите нули функции.
в)Найдите наибольшее и наименьшее значение функции.

Answer 1

$y= frac{x}{|x|}+x^3+x+x^2\\y(-x)= frac{-x}{|-x|}+(-x)^3+(-x)+(-x)^2=\\ =-frac{x}{|x|}-x^3-x+x^2= -( frac{x}{|x|}+x^3+x-x^2) neq -y(x) neq y(x)$

y=f(x)- ни чётна, ни нечётна

2-я задача во вложении!