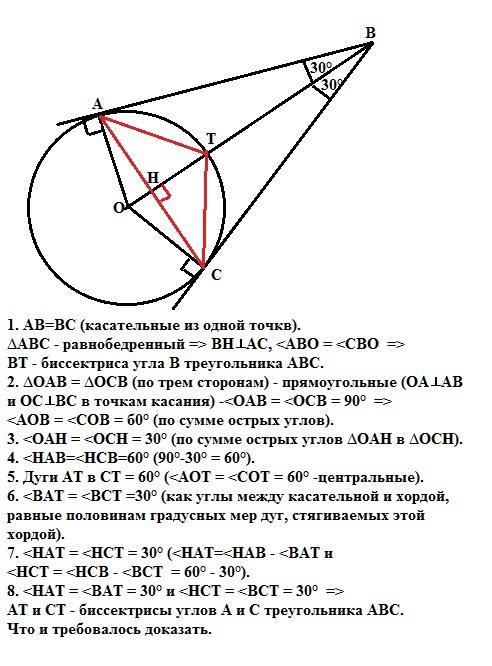
Прямые АВ, ВС- касательные к окружности,центром которой является точкаО,точкиА и С точки касания.Окружность пересекает отрезок ОВ в точке Т.Угол АВТ=30гр.Докажите,что точка Т является точкой перессечения биссектрис треугольника АВС
Ответы
Объяснение:
1. АВ=ВС (касательные из одной точки).
∆АВС - равнобедренный => ВН⊥АС, <АВО = <СВО =>
ВТ - биссектриса угла В треугольника АВС.
2. ∆ОАВ = ∆ОСВ (по трем сторонам) - прямоугольные (ОА⊥АВ и ОС⊥ВС в точкам касания) -<ОАВ = <ОСВ = 90° =>
<АОВ = <СОВ = б0° (по сумме острых углов).
3. <ОАН = <ОСН = 30° (по сумме острых углов ∆ОАН в ∆ОСН).
4. <НАВ=<НСВ=60° (90°-30° = 60°).
5. Дуги АТ в СТ = 60° (<АОТ = <СОТ = 60° -центральные).
6. <BAT = <BCT =30° (как углы между касательной и хордой, равные половинам градусных мер дуг, стягиваемых этой хордой).
7. <HAT = <HCT = 30° (<HAT=<HAB - <BAT и
<HCT = <HCB - <BCT = 60° - 30°).
8. <HAT = <BAT = 30° и <HCT = <BCT = 30° =>
АТ и СТ - биссектрисы углов А и С треугольника АВС.
Значит точка Т - точка пересечения биссектрис углов треугольника АВС, что и требовалось доказать.