Question

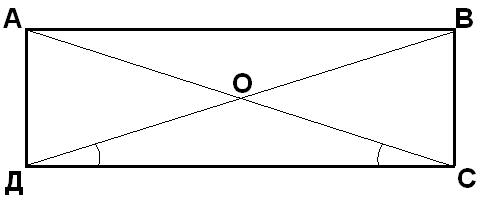
Диагональ делит угол прямоугольника в отношении 1:8. Найти углы между диагоналями прямоугольника.

Answer 1

См. рисунок. По условию <ВДС равен одной условной единице, <АДВ равен восьми условным единицам. Тогда <АДС = <ВДС + <АДВ = 1 + 8 = 9 условных единиц. С другой стороны этот угол прямой, поскольку фигура-прямоугольник, следовательно, в градусах <АДС = 90 градусов. Отсюда можно найти величину одной условной единицы в градусах  90/9 = 10 градусов. Таким образом, <ВДС = 10 градусов. <АСД = <ВДС = 10 град. Теперь можно найти < ДОС. Сумма углов в любом треугольнике равна 180 градусов. Следовательно, < ДОС = 180 -10 – 10 = 160 градусов.  < ДОС = < АОВ .т.к. эти углы вертикальные. Поскольку сумма всех четырех углов, образованных пересечением диагоналей равна 360 градусов, можно найти сумму остальных двух углов <АОД и <ВОС. <АОД + <ВОС = 360 -160 – 160 = 40 градусов. Поскольку <АОД и <ВОС являются вертикальными углами, то они равны между собой, и каждый из них = 40/2 = 20 градусов.