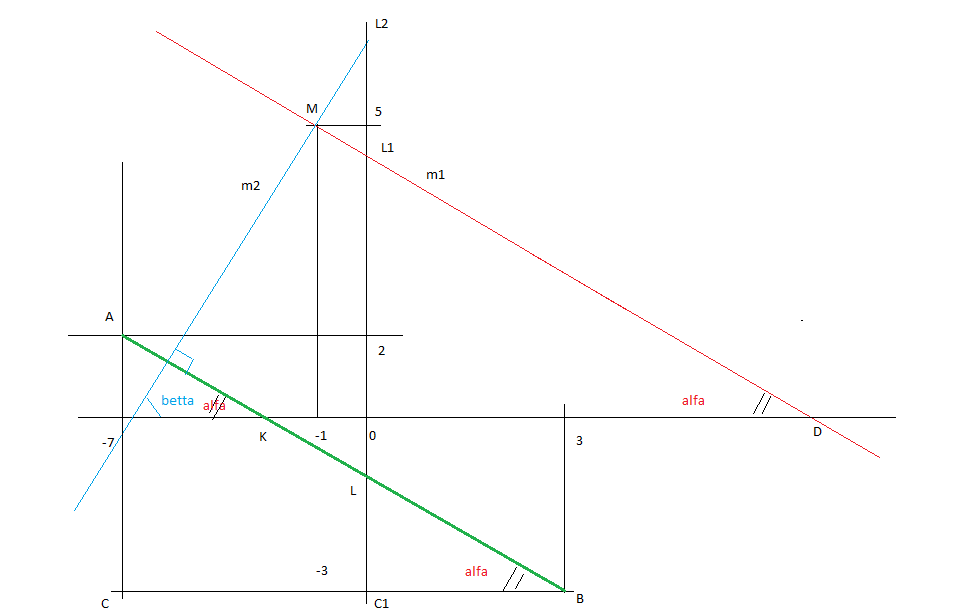
составить уравнение прямых, проходящих через точку М(-1;5) параллельно и перпендикулярно к отрезку АВ, если А(-7;2) и В(3;-3)
Ответы
уравнение прямой - стандартный вид у=kx+b
k - угловой коэффициент - его надо найти
я сделаю рисунок , чтоб было понятно
треугольник ABC - Прямоугольный
РЕШЕНИЕ
Найдем уравнение прямой АВ
угловой коэффициент
k= tg(alfa) = АC/ВC = ( Y(A) - Y(C)) / ( X(B)-X(С) ) = (2-(-3)) / (3-(-7)) = 5/10 =0.5
Тангенс угла alfa имеет отрицательное значение для данной прямой
k= - 0.5
значение b - точка пересечения АВ с осью ОУ
треугольники ABC ~ LBC1 подобные
LC1 /AC =BC1/BC
LC1 = BC1/BC *AC
подставим координаты точек
LC1 = BC1/BC *AC =3/(3+7)*(3+2)=3/2=1.5
тогда b= 0L = 0C1-LC1=-3-(-1.5)=-1.5=-3/2
Уравнение прямой АВ
y=-0.5x-1.5 или y=-1/2*x-3/2 или y=-(x+3)/2
Уравнение прямой m1 параллельной АВ
так как они параллельны
угловой коэффициент k - тот же k=-0.5
значение b - точка пересечения m1 с осью ОУ -точка L1
b=Y(M)-0L=5-1.5=3.5
Уравнение прямой m1
y=-0.5x+3.5 или y=-1/2*x-7/2 или y=-(x+7)/2