Question

Докажите, что параллелограмм, у которого высоты, проведенные из вершины острого угла, равны, является ромбом.

Answer 1

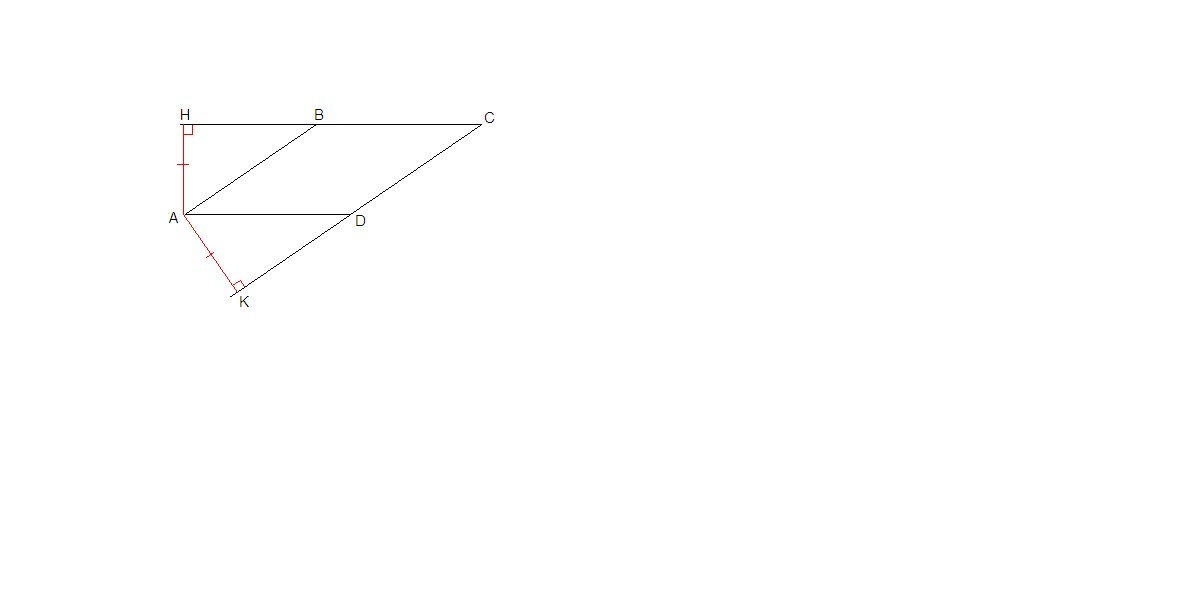
Проведем АН⊥ВС и АК⊥CD.
∠АВН = 180° - ∠АВС
∠ADK = 180° - ∠ADC так как углы смежные.
В параллелограмме противоположные углы равны. Поэтому ∠АВС = ∠ADC, значит и ∠АВН = ∠ADK.
ΔАВН = ΔADK по катету и противолежащему острому углу (АН = АК по условию, ∠АВН = ∠ADK).
Тогда равны и гипотенузы этих треугольников.
AB = AD.
В параллелограмме противолежащие стороны равны, значит
AB = AD = CD = BC, ⇒
ABCD - ромб.