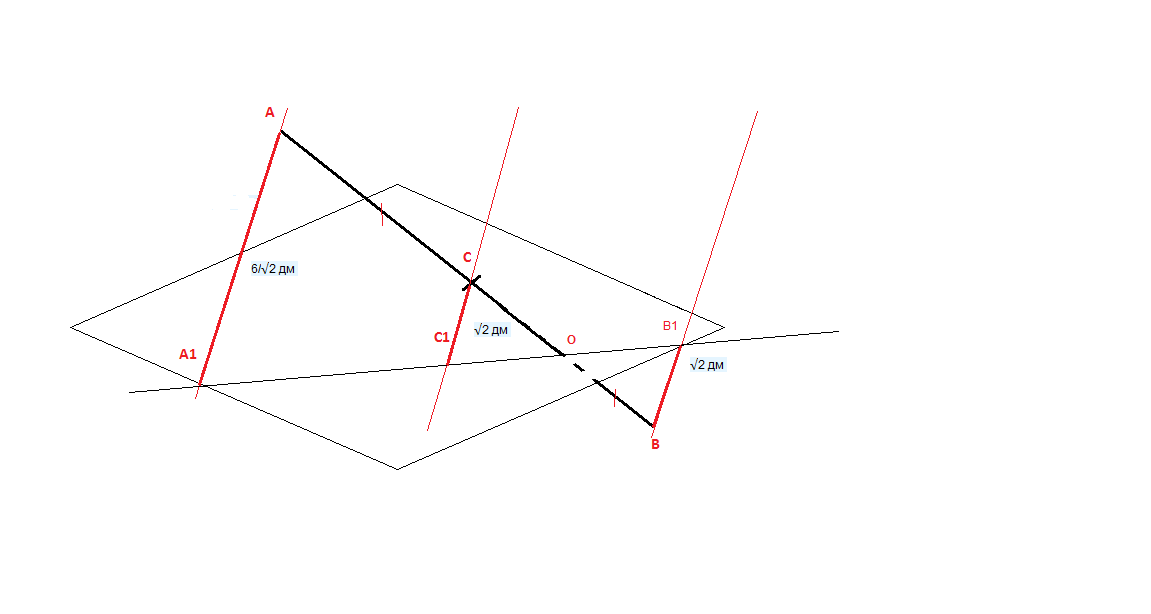
Отрезок AB пересекает плоскость альфа ,точка C - середина AB .Через точки A B C проведены паралеьные прямые пересекающие плоскость альфа в точках A₁ C₁ B₁ найдите CC₁ ,если AA₁ = 6/√2 дм и BB₁ = √2 дм (дециметр)
Ответы
РЕШЕНИЕ
AA₁ = 6/√2 дм =3√2 дм
BB₁ = √2 дм
< АОА1 и <BOB1 вертикальные -равны
АА1 || BB1 || CC1 - параллельные
указанные прямые отсекают на АВ и А1В1 пропорциональные отрезки
Это следствие из теоремы Фалеса о параллельных прямых пересекающих стороны угла.
тогда треугольники AOA1 ~ COC1 ~BOB1 подобные
AO/OB=AA1/BB1=3√2 /√2 = 3 : 1
пусть АВ=х
тогда
АО=3/4 х
ОВ= х
АС=СВ= 1/2 х
СО= АО-АС=3/4 х - 1/2 х=3/4 х - 2/4 х=1/4 х
теперь снова треугольники AOA1 ~ COC1 подобные
AA1/СС1= AO/СO=3/4х / 1/4х = (3/4) / (1/4) = 3 : 1
CC1=1/3 * AA1 = 1/3 *3√2 =√2 дм (возможна запись 1/3 *6/√2 = 2/√2 дм )
Ответ √2 дм или 2/√2 дм