Question

четырехугольник ABCD вписан в окружность. на продолжении диагонали BD за точку D выбрана точка F такая, что AF || BC. докажите, что окружность, описанная около треугольника ADF касается прямой AC

Answer 1

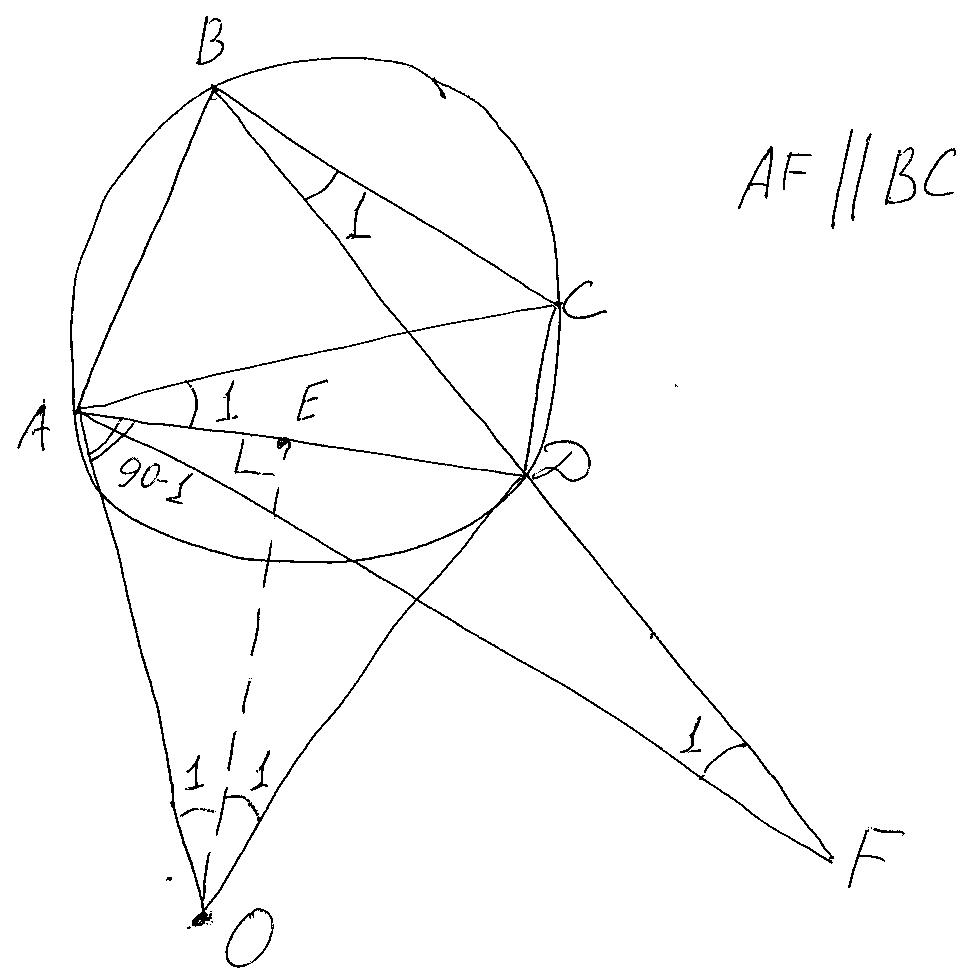
Проведём радиусы ОА и ОД  окружности описанной около треугольника АDF(смотри рисунок). Угол АОД окружности (на рисунке не показана)-центральный, а АFД –вписаный. Но они оба опираются на одну дугу АД. То есть угол АОД в два раза больше угла АFД(условно обозначен 1). Треугольник АОД- равнобедренный(АО и ОД радиусы), высота ОЕ делит угол АОД пополам. Отсюда угол ОАЕ=90-угол1. Далее- угол  СВД равен углу АFВ как накрест лежащие поскольку АF параллельна ВС. Но угол СВД равен углу САД поскольку они оба опираются на дугу СД. Тогда угол ОАС =угол САД+ угол ОАД=угол1+угол90-угол1=90градусов. То есть радиус ОА окружности описанной около АДF перпендикулярен АС. А это значит , что окружность касается этой прямой.