Question

в равнобедренную трапецию с основаниями 2 и 8 см вписана окружность, найдите боковую сторону трапеции, радиус окружности и площадь

Answer 1

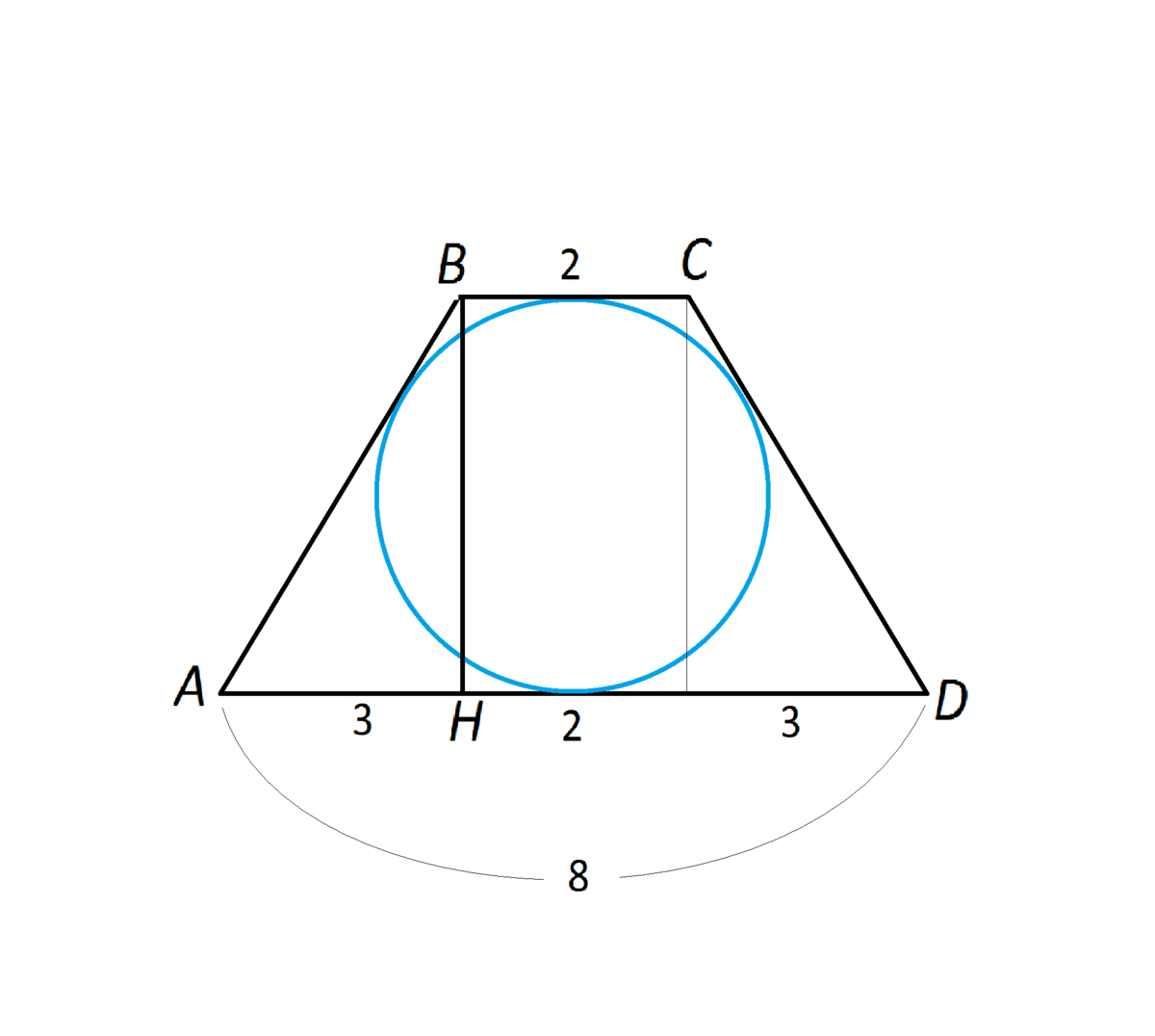
Окружность можно вписать только в такой четырехугольник, в котором суммы противоположных сторон равны.
Трапеция - четырехугольник. 
Трапеция по условию равнобедренная, следовательно, ее боковые стороны равны между собой. 
АВ=СD=(АD+ВС):2
АВ=(2+8):2=5 см
Радиус вписанной в трапецию окружности равен половине высоты трапеции. 
Опустим из В высоту к основанию АD.
Высота равнобедренной, проведенная из тупого угла, трапеции делит большее основание на два отрезка, из которых меньший равен полуразности оснований, а больший - их полусумме. 
АН=(8-2):2=3 см
Треугольник АВН -«египетский», катет ВН=4 ( проверьте по т. Пифагора). 
Следовательно, 
r=4:2=2 см
Площадь трапеции равна половине произведения ее высоты на сумму оснований. 
S (ABCD)=4*(2+8):2=20 cм²
Площадь круга находят по формуле 
S=πr²
S=π*2²=4π см² или 4*3,14= примерно 12, 56 см²