Предмет: Геометрия,
автор: inna01
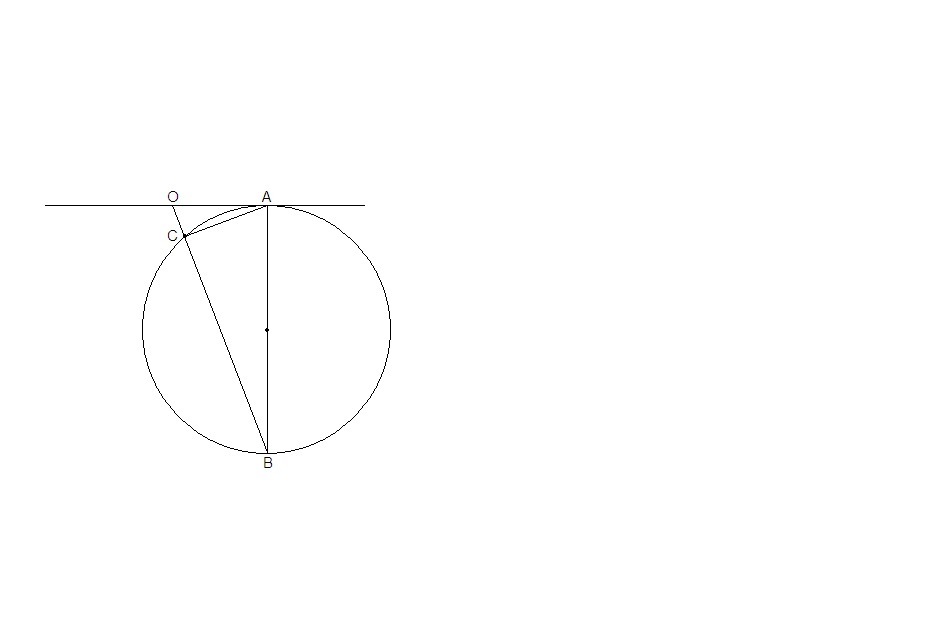
Отрезок АВ - диаметр окружности, прямая ОА - касательная к окружности, а прямая ОВ пересекает окружность в точке С. Вычмслить градусную меру углов, если известно что дуга ВС - дуга АС = 40°
Ответы
Автор ответа:
0
Решим задачу с дополненным условием:
Знак ∪ использован, как знак дуги.
По условию ∪ВС - ∪АС = 40°, а ∪ВС + ∪АС = 180°, так как АВ - диаметр.
∪АС = (180° - 40°)/2 = 70°.
∪ВС = ∪АС + 40° = 110°
∠АВС вписанный, опирается на дугу АС, значит
∠АВС = ∪АС/2 = 70°/2 = 35°.
∠ВАС вписанный, опирается на дугу ВС, значит
∠ВАС = ∪ВС/2 = 110°/2 = 55°
Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому ∠ОАВ = 90°.
∠ОАС = ∠ОАВ - ∠ВАС = 90° - 55° = 35°
Вписанный угол, опирающийся на полуокружность, прямой. Поэтому
∠АСВ = 90°.
∠АСО = ∠АСВ = 90° как смежные.
ΔАОС: ∠АСО = 90°, ∠ОАС = 35°
∠АОС = 90° - 35° = 55° так как сумма острых углов прямоугольного треугольника 90°.
Знак ∪ использован, как знак дуги.
По условию ∪ВС - ∪АС = 40°, а ∪ВС + ∪АС = 180°, так как АВ - диаметр.
∪АС = (180° - 40°)/2 = 70°.
∪ВС = ∪АС + 40° = 110°
∠АВС вписанный, опирается на дугу АС, значит
∠АВС = ∪АС/2 = 70°/2 = 35°.
∠ВАС вписанный, опирается на дугу ВС, значит
∠ВАС = ∪ВС/2 = 110°/2 = 55°
Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому ∠ОАВ = 90°.
∠ОАС = ∠ОАВ - ∠ВАС = 90° - 55° = 35°
Вписанный угол, опирающийся на полуокружность, прямой. Поэтому
∠АСВ = 90°.
∠АСО = ∠АСВ = 90° как смежные.
ΔАОС: ∠АСО = 90°, ∠ОАС = 35°
∠АОС = 90° - 35° = 55° так как сумма острых углов прямоугольного треугольника 90°.
Приложения:
Автор ответа:
0
прокомментирую, т.к. решение добавить нельзя. Согласно рисунка величина дуги СВ будет 2А (где А- величина угла А) аналогично величина дуги АС будет 2В. Получаем систему двух линейных уравнений 1) 2А-2В=40 2)А+В=90 откуда А=55 В=35 это такое же решение, только "в профиль"
Похожие вопросы
Предмет: Экономика,
автор: 221bsherlockholmes
Предмет: Литература,
автор: lilialsafova6533
Предмет: Английский язык,
автор: Аноним
Предмет: Физика,
автор: Sazonov