Question

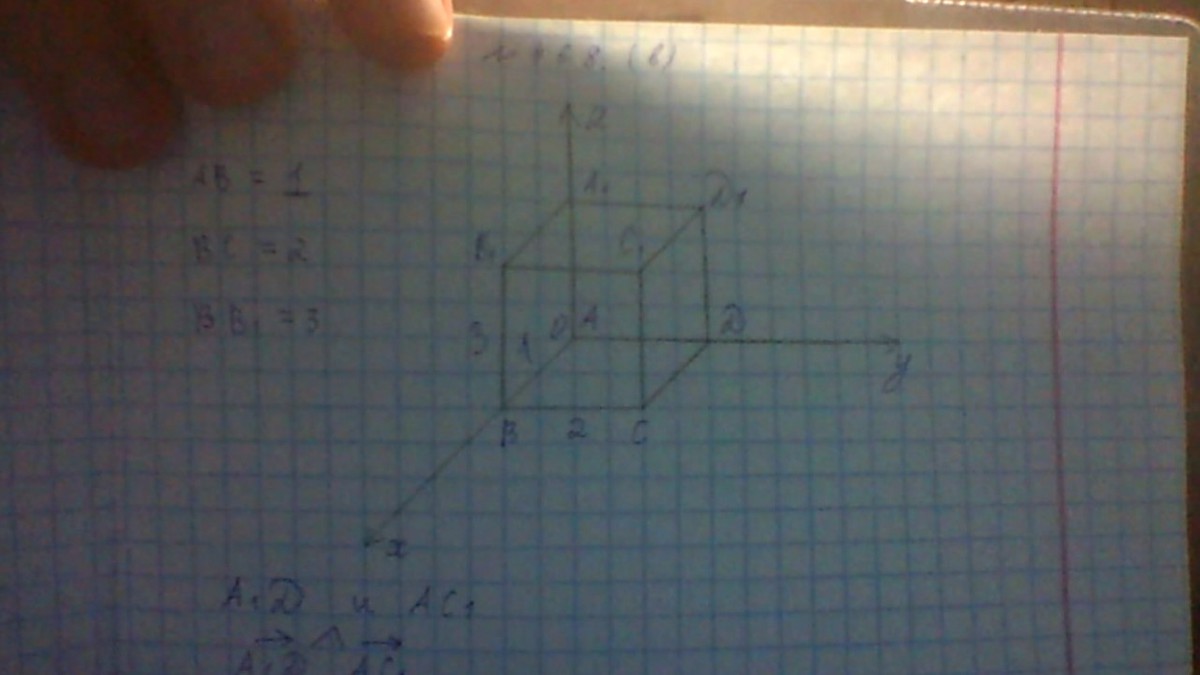
Вычислить косинус угла между прямыми  А1D и AC1
По моему дано, чтобы буквы были раставленны , как у меня

Answer 1

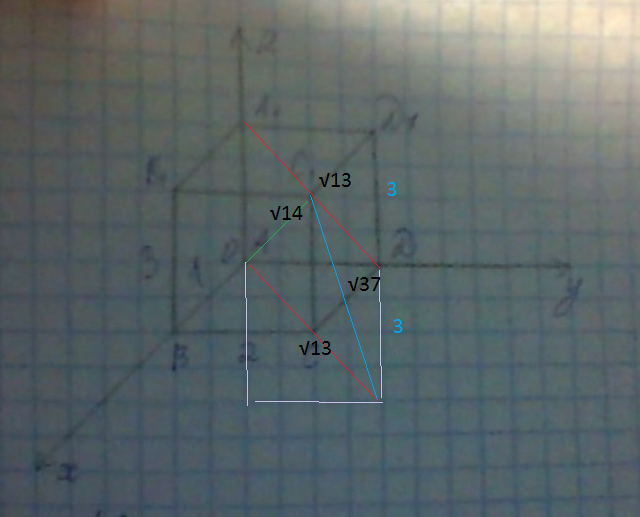
Перенесем прямую A₁D  в точку А
Искомый угол - угол треугольника со сторонами
√13; √14 и √37
По теореме косинусов
(√37)²=13+14-2√13·√14 ·сosα    ⇒
$cos alpha = frac{13+14-37}{2 sqrt{13}cdot sqrt{14} }$

Answer 2

Задачу можно решить векторным методом. Для этого надо "привязать" данный параллелепипед к осям координат, определить координаты его вершин и найти угол между векторами АС и D1B по известной формуле: cosα = {a•b}/|a|•|b| или cosα=(x1•x2+y1•y2+z1*z2)/[√(x1²+y1²+z1²)*√(x2²+y2²+z2²)].

Answer 3

я забыл, честно

Answer 4

я просто думал этот метод самый популярный

Answer 5

НАфань , помогите!!!!

Answer 6

Координаты точек  А(0,0,0,) ,  А1(0,0,3) ,  D(0,2,0),  C1(1,2,3)
Координаты векторов: А1D=( 0,2,-3) ,  AC1=(1,2,3,)

$cos alpha =frac{0+4-9}{sqrt{4+9}cdot sqrt{1+4+9}}=frac{-5}{sqrt{13}cdot sqrt{14}}\\ alpha =pi -arccos frac{5}{sqrt{182}}$

Answer 7

почему у вас 1 2 3 ????