Question

ПОМОГИТЕ!!
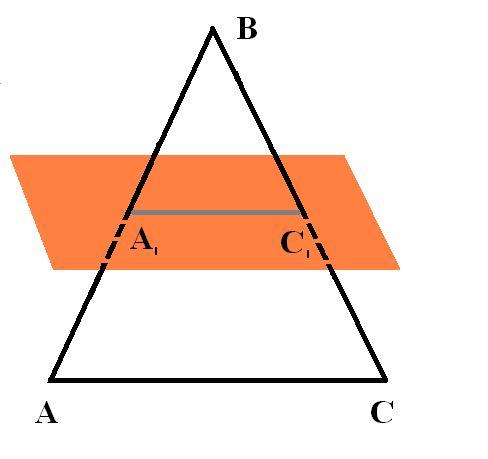
Дан треугольник ABC. Плоскость, параллельная прямой АС, пересекает сторону АВ в точке А1, а сторону ВС в точке С1. Вычислите длину отрезка АА1, если ВС:BC1 = 9:5. AB = 27 см
С РИСУНКОМ ПОЖАЛУЙСТА!

Answer 1

Так как проведенная плоскость параллельна стороне АС, то А₁С₁||AC. Значит, треугольники АВС и А₁BС₁ подобны по двум соответственным углам при параллельных прямых. Составляем отношение сторон:
$frac{AB}{A_1B}= frac{BC}{BC_1} \ A_1B= frac{ABcdot BC_1}{BC} \ A_1B= frac{27cdot 5x}{9x} =15 \ AA_1=AB-A_1B \ AA_1=27-15=12(sm)$
Ответ: 12 см

Answer 2

а какой рисунок будет?

Answer 3

спасибо!