Question

Помогите! Как решаются задачи по нахождению угла, изображенного на клетчатой бумаге?

Answer 1

возможны варианты...
1) можно попытаться построить прямоугольный треугольник по линиям сетки, визуально (по клеточкам) посчитать длину катетов,
или (если по клеточкам посчитать не представляется возможным) 
вычислить длину сторон треугольника как длину ДИАГОНАЛИ прямоугольника...
Вершины (точки) обычно заданы в узлах сетки,
длину сторон прямоугольника по сетке определить всегда можно,
диагональ вычислить по т.Пифагора)))
а дальше записать какую-нибудь тригонометрическую функцию угла (как отношение сторон прямоугольного треугольника)))
2) бывает, что построенный треугольник НЕ прямоугольный... тогда нужно применить теорему косинусов)))
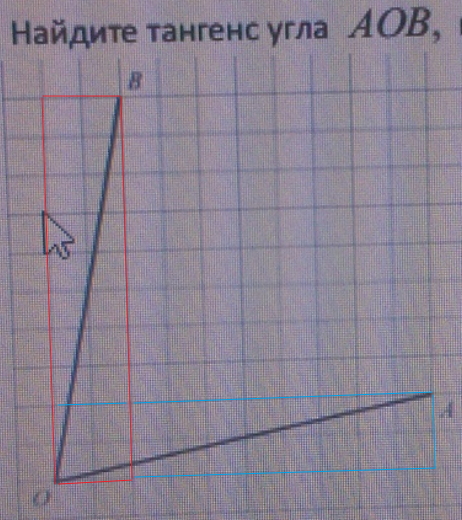
например, ОВ -- диагональ прямоугольника со сторонами 2 и 10
ОВ = √104 = 2√26
ОА = ОВ
АВ = √(64+64) = 8√2
и вот в этом примере высоту построить по линиям сетки не представляется возможным, поэтому по т.косинусов можно записать:
AB² = AO² + OB² - 2*AO*OB*cos(AOB)
cos(AOB) = (2*104 - 128) / (2*104) = 80/208 = 10/26 = 5/13
зная косинус, можно найти синус...
sin(AOB) = √(1 - 5²/13²) = √(144/13²) = 12/13
tg(AOB) = (12/13) / (5/13) = (12/13) * (13/5) = 12/5 = 24/10 = 2.4
как-то так...