Question

докажите что параллелограмм является прямоугольником если диагонали образуют равные углы с одной из его сторон

Answer 1

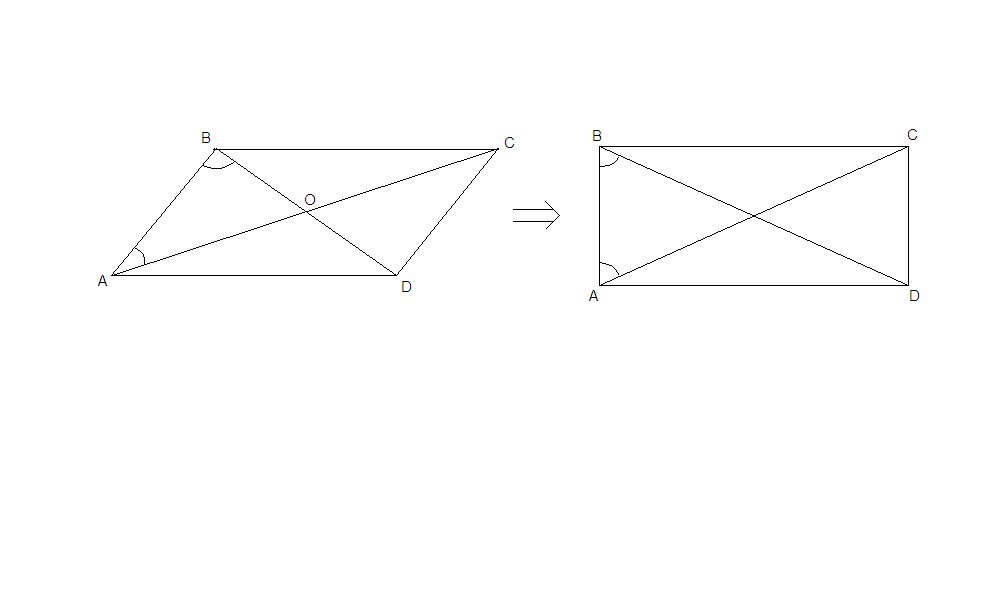
Пусть равны углы, которые диагонали образуют со стороной АВ,
∠ОАВ = ∠ОВА.
Тогда ΔОАВ равнобедренный, ОА = ОВ.
Диагонали параллелограмма точкой пересечения делятся пополам, значит и
АС = BD.
Если в параллелограмме диагонали равны, то это прямоугольник.