Question

Вычислите объем правильной треугольной пирамиды, сторона основания которой 6 см, высота 9 см

Answer 1

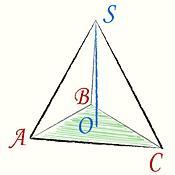
Дано:  SABC- правильная пирамида, SO- высота, SO=9 см, AB=Bc=AC=6 см.

Решение:

$V=frac{1}{3} S_{o}h=frac{1}{3}(frac{1}{2}*frac{sqrt{3}a }{2} *a )h=frac{1}{3}*frac{sqrt{3}a^2 }{4}*h=frac{1}{3}*frac{sqrt{3}*6^2 }{4}*9=frac{9*36*sqrt{3} }{3*4} =9*3*sqrt{3} =27sqrt{3}$см³

Ответ: 27√3 см³

Использовались формулы:

1) Объем пирамиды $V=frac{1}{3} S_oh$

2) Площадь треугольника: $S=frac{1}{2} ah$

3) высота равностороннего треугольника: $h=frac{sqrt{3} }{2} a$