Предмет: Математика,
автор: Darina3645
Помогите,пожалуйста,решить
Приложения:
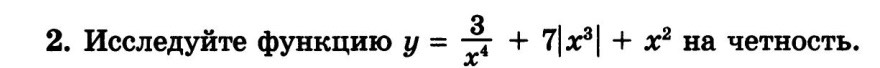
Ответы
Автор ответа:
0
Функция является чётной, если для всех значений x из области определения f(x)=f(-x).
В нашем случае функция определена везде, кроме точки x=0.

 , значит,
, значит,  при любом
при любом  . Следовательно, функция является чётной.
. Следовательно, функция является чётной.
В нашем случае функция определена везде, кроме точки x=0.
Похожие вопросы
Предмет: Физика,
автор: anna2004mau1
Предмет: Русский язык,
автор: strukov9090
Предмет: Химия,
автор: Sonechka2304
Предмет: Математика,
автор: alex2479
Предмет: История,
автор: natalipa2010