Предмет: Алгебра,
автор: Ablai97
Задания во вкладках..........
Приложения:
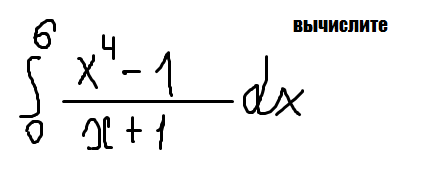
Ответы
Автор ответа:
0
Упростим вначале выражение:

Возьмем интеграл:

Возьмем интеграл:
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: fajtpolina14
Предмет: Информатика,
автор: lasikokov1999
Предмет: Английский язык,
автор: anastasiya722kas
Предмет: Математика,
автор: maxxxlogik