Предмет: Алгебра,
автор: anastasiarifma
Задание по алгебре, помогите решить, пожалуйста.
Приложения:
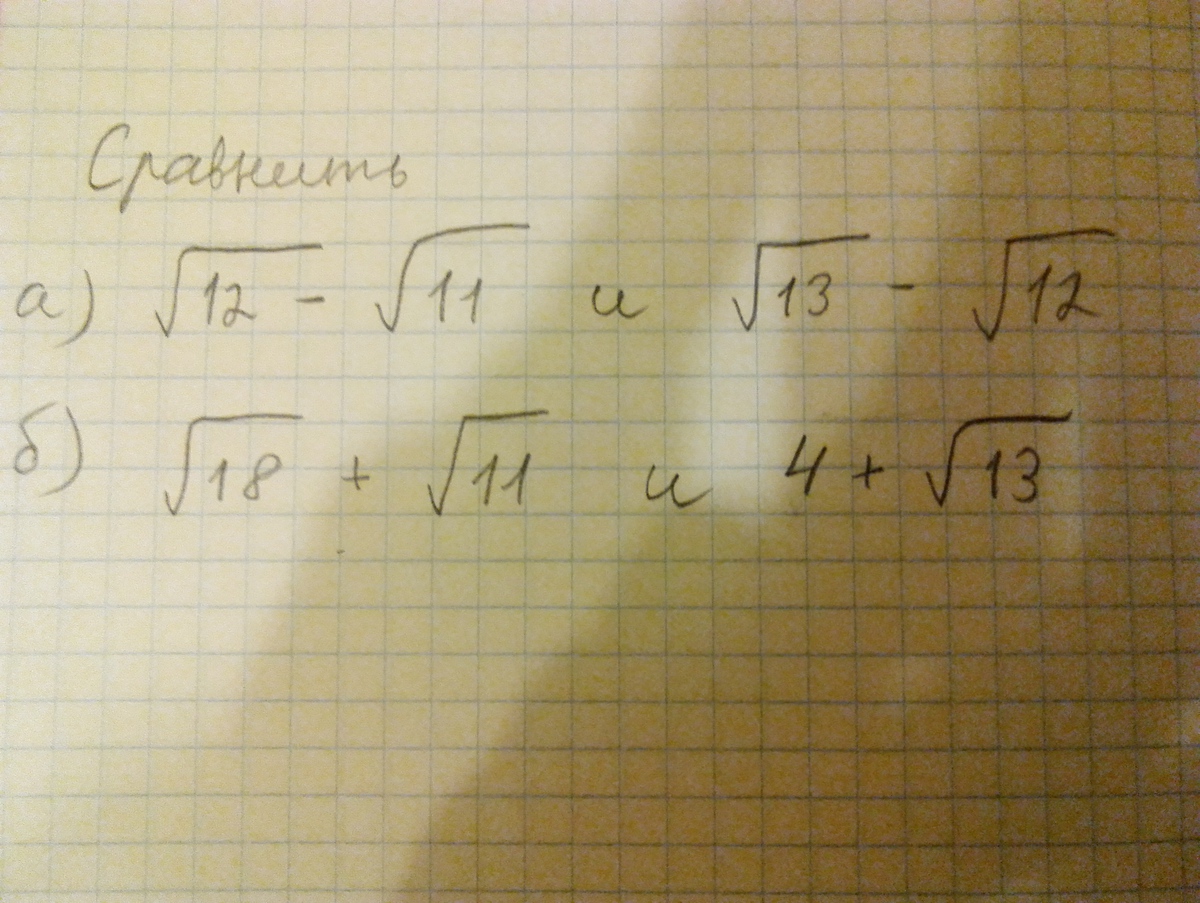
Ответы
Автор ответа:
0
Так как слева и справа стоят положительные числа, то возводим левую и правую часть в квадрат.
Опять слева и справа положительные числа, возводим в квадрат:
Автор ответа:
0
Спасибо огромное!
Похожие вопросы